贾佳亚团队的最新研究：运用10k数据提升大模型的数学技能，超越GPT-4水平。

编辑日期：2024年07月05日

运用类似教导学生的技巧，训练大型语言模型能取得显著成效。

中国香港中文大学贾佳亚团队提出了一个创新策略，他们将推理步骤融入大模型的优化过程中，仿佛在亲自指导模型学习。仅仅使用10,000条数据，该方法便能使大模型的数学能力提升5.6%。

通过这种技术，拥有720亿参数的Qwen模型在数学表现上超过了包括GPT-4、Gemini1.5-Pro和Claude3-Opus在内的多个未开源模型。

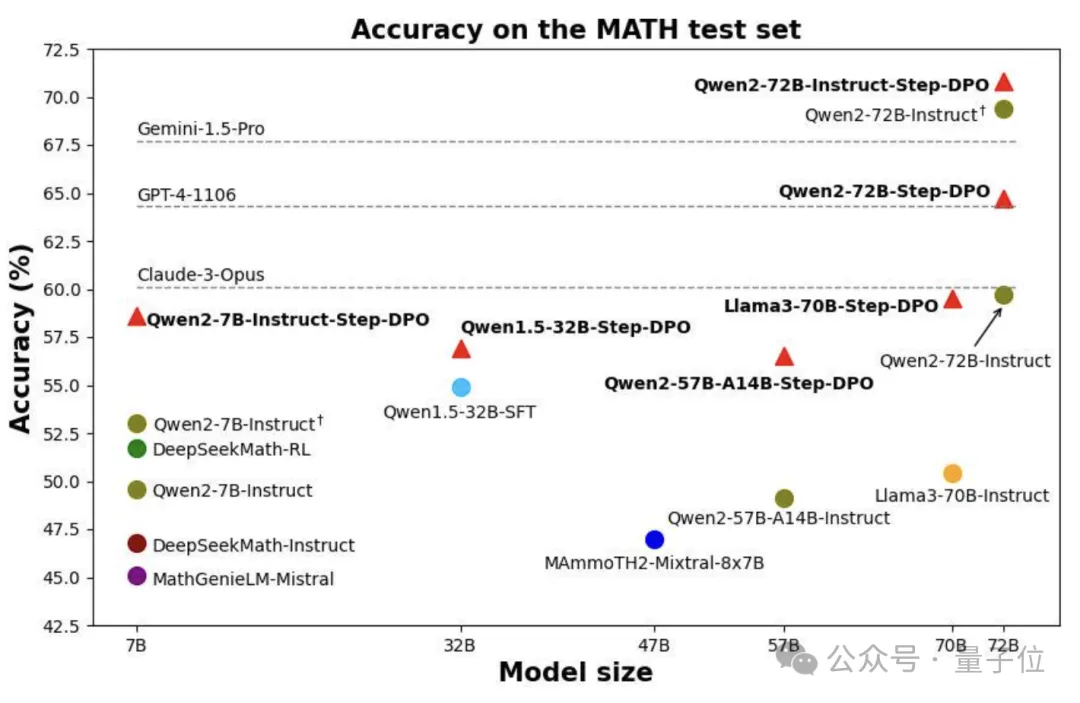
贾佳亚团队深入借鉴了教育中的纠错理念，他们对斯坦福团队的DPO（直接偏好优化）进行了细致的改进，发展出Step-DPO这一逐步执行的策略。这一创新显著提升了Qwen-72B模型在多种数据集上的表现，同时增强了它处理复杂长链推理任务的能力。

强化推理能力是大型语言模型领域的一大挑战。通常，思维链策略通过在提示中加入“让我们一步步思考。”来引导模型逐步推理。不过，面对复杂问题，仅靠修改提示往往不足以确保模型得出正确答案，因为这类问题可能需要数十步的推理过程，任何一步失误都会导致最终结果偏离。

现有的解决方案试图通过监督式微调（SFT）阶段增加问答数据以增进模型的对齐性。但当SFT数据量达到一定规模时，模型容易产生幻觉，性能增长也趋于停滞。原因可能是随着偏好输出概率的提高，非偏好输出的概率也随之增加。

为了解决这个问题，斯坦福大学提出了直接偏好优化方法。它通过构建基于人类偏好的数据集，每个样本包含一个输入提示、一个优选输出和一个非优选输出。然后，模型直接进行微调，以最大化生成优选输出的概率，同时最小化非优选输出的概率。因此，DPO的优化目标就在于此。

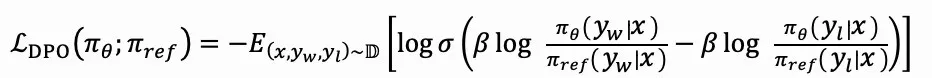
πθ和πref分别代表当前的微调模型及参照模型。然而，在涉及复杂连锁推理的任务中，DPO方法无法精确识别出推理过程中的错误环节，因此难以定位关键的失误步骤。

如图所示，使用DPO的模型在训练时难以确切评估推理步骤的正确性。

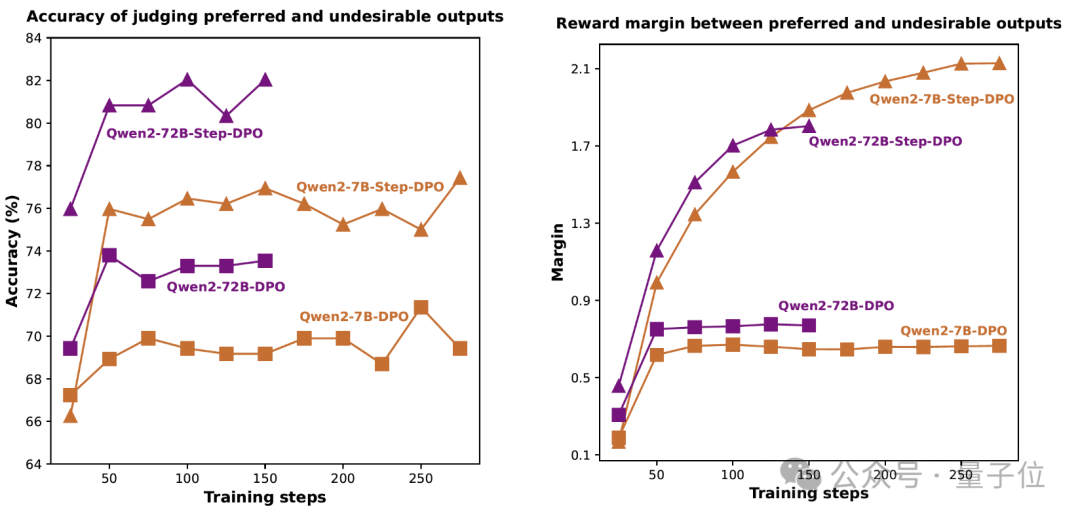
于是，作者提出了一种创新的方法，称为基于推理过程的直接偏好优化——Step-DPO。

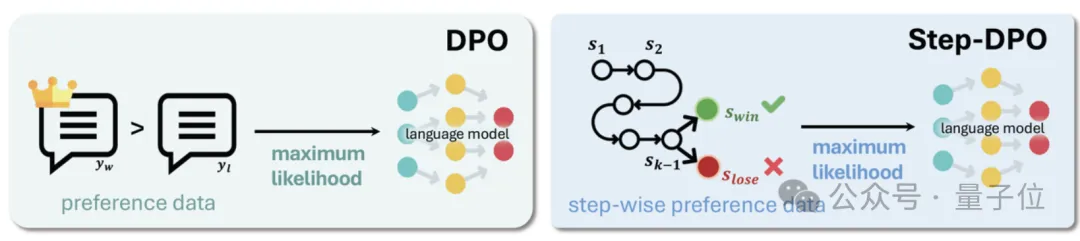
如同教师指导学生改正错误，不仅指出最终结果的谬误，还会明确指明在哪一步出现了问题，以便学生迅速修正。类比于此，Step-DPO不再全面地与DPO比较最终答案，而是将每个推理过程视为独立的模块，并逐一评估这些步骤，从而在更细致的层面上提升模型的多步推理分析能力。

Step-DPO的优化目标聚焦于：

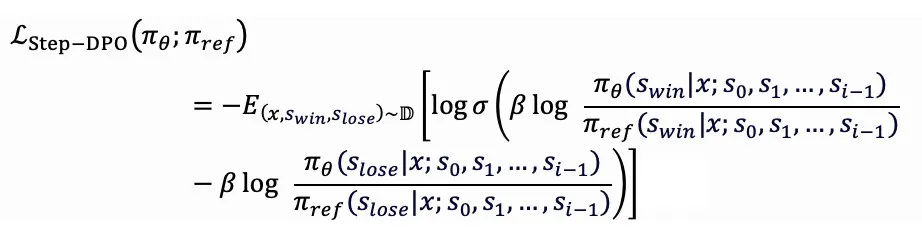
作者还提倡了一种创新的数据处理方法，其流程主要由三个阶段构成，如下图所示：

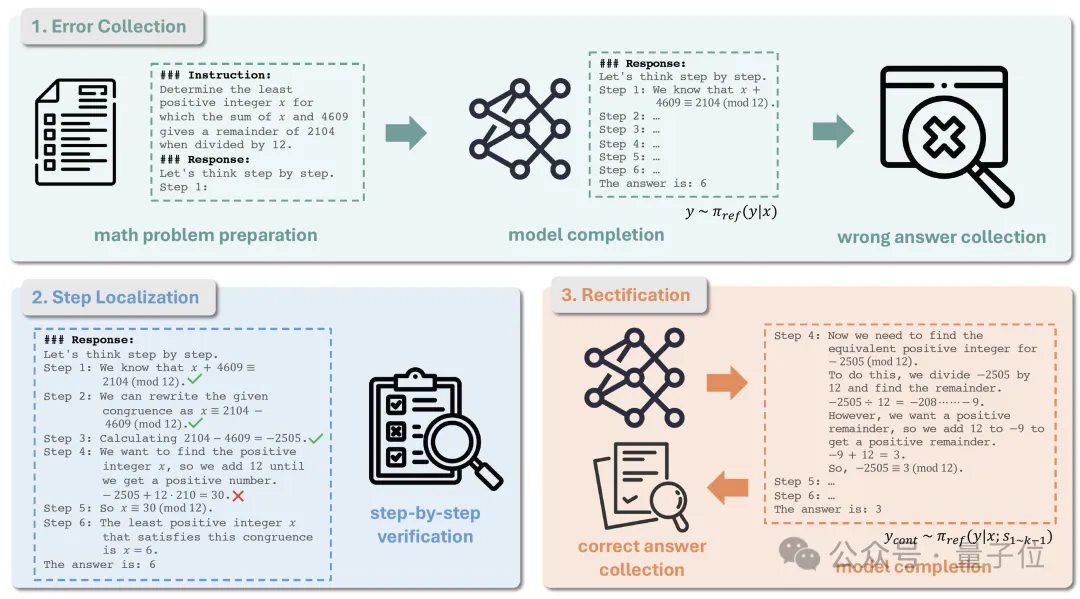
首要任务是失误汇集。

首先，设定一个数学问题集合D0，它包含元素对(x, y)，其中x代表数学题目，而y是其准确解答。

接下来，利用基础模型πref来获取每个数学问题x的解决方案。

在模型推断阶段之前，需在问题前插入思考链（CoT）前缀作为引导，目的是使模型的推理过程结构化，表现为一系列以“步骤i：”开头的推理步骤。

模型推理后，我们得到每个问题x的推断结果y。接着，我们聚焦于那些与正确答案y*不符的结果，并将它们整合成新的数据集D1。

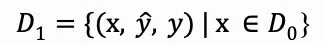
第二步涉及识别错误的推理过程。

每个预测错误的结论y都是由一系列推理步骤构成的序列，即y=s1,s2,…,sn。接下来，我们需要通过人工检查或运用GPT-4来逐一验证这些步骤的准确性，目标是找出首个出错的步骤sk，它的序号会被记录下来。

一旦找到这个错误步骤sk，我们将其标识为错误推理步骤slose，由此定义了D2。

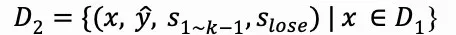
最后是纠正错误的步骤。

要为D2中的每个样本获取准确的推理过程，我们需要运用模型πref进行推断。在这一过程中，利用提示信息x和先前正确的推理步骤s1到s_k-1，我们对可能的后续输出ycont进行多次采样。这个操作可以被描述为：

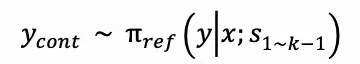
接下来，我们选择ycont中与实际答案匹配的输出，并将这些匹配中的首个推理过程标记为swin，最终形成数据集D。

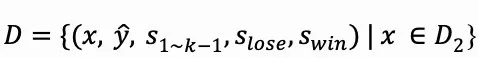
下图呈现了一个典型的数据样例。值得关注的是，这个数据处理过程几乎不需要大量人力参与，无论是人类还是GPT-4，其主要任务仅在于评估提供的推理步骤的准确性，而无须直接生成答案来纠正错误。

通过在SFT模型或现有的开源Instruct模型上执行Step-DPO微调，只需少量的10,000条数据和数百次训练迭代，就能显著增强数学处理能力。

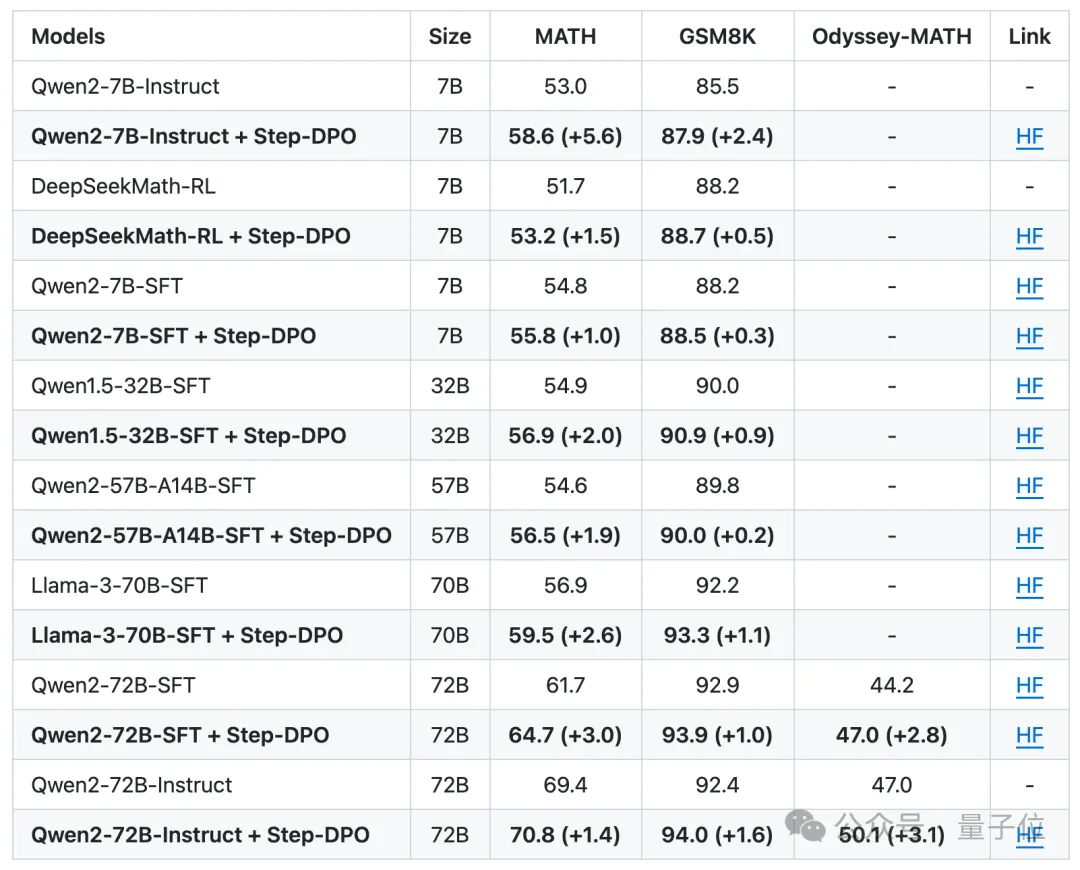
如图所示，基于Qwen2-7B-Instruct模型应用Step-DPO后，MATH基准测试的准确性可提升5.6%。

而在更为庞大的Qwen2-72B-Instruct模型上使用Step-DPO，其在MATH和GSM8K测试集的准确率分别达到了70.8%和94.0%，超越了诸如Gemini-1.5-Pro、GPT-4-1106及Claude-3-Opus等非开源模型。

值得注意的是，即使是在包含高难度数学竞赛题目的Odyssey-MATH排行榜上，Step-DPO也表现出明显的改进。

经过优化的Step-DPO方法使模型更为稳健，显著降低了出现幻觉的概率，同时在推断阶段也减少了错误的发生。以下示例展示其效果：

设函数h(x)等于f-1(x)，已知h(2)=10，h(10)=1，h(1)=2，试求解f(f(10))的值。

求满足条件的整数t，其平方根应在2和3.5之间，这样的t值有几个？

即使是面对如下所示的数学竞赛难题，经过Step-DPO处理的模型也能成功解答。

在所有从集合{1,2,...,10}到自身且不单调递增的函数f中，存在一些函数拥有不动点，而另一些则不具备，这两种情况的数量差异是多少？

目前，该项目已将源代码、数据集、模型实例及演示Demo公开在GitHub和Hugging Face平台上，用户可方便地进行在线体验。

论文链接： https://arxiv.org/abs/2406.18629 GitHub仓库： https://github.com/dvlab-research/Step-DPO 在线演示： http://103.170.5.190:7870/ 模型库（Hugging Face）： https://huggingface.co/collections/xinlai/step-dpo-6682e12dfbbb2917c8161df7 数据集（Hugging Face）： https://huggingface.co/datasets/xinlai/Math-Step-DPO-10K