仅需唤醒3.8B个参数,其效能媲美同等7B规模的模型!无论是训练还是微调场景皆适用,源自微软技术,精准响应需求。
编辑日期:2024年07月22日
一项革新性的发现——“扩展法则”推理优化策略浮出水面,揭示了仅需调动模型60%参数,即可媲美全参数激活的密集型模型效能的秘密。这一突破源自微软亚洲研究院,他们成功实现了模型的全面稀疏激活,显著降低了推理成本,且应用场景广泛,无论是初始训练、后续训练还是微调阶段,均能发挥卓越效能。
名为Q-Sparse的这一创新方法,巧妙地在神经元层面实施模型稀疏化,相较于传统手段,其精细化操作在保持相同推理成本的同时,性能与稀疏率表现更胜一筹。其中,“Q”代表量化,表明该技术不仅适用于标准模型,还兼容量化技术,可适配各类量化模型。研究者指出,Q-Sparse与量化技术的融合,将释放更大的成本效益空间。
在探索Q-Sparse的过程中,研究团队还深入剖析了参数规模、稀疏率与模型性能间的内在联系,提炼出了专为推理优化设计的“扩展法则”。网友对此反响热烈,称其超越了ReLU,展现出巨大潜力。
更有用户寄希望于技术普及速度,期待AMD的ROCm能够超越NVIDIA,率先拥抱Q-Sparse,加速其应用进程。Q-Sparse的核心机制在于,对输入张量施以Top-K稀疏化函数,精准筛选关键信息,实现高效推理。
综上所述,Q-Sparse不仅革新了模型稀疏化技术,还揭示了参数、稀疏率与性能间的新规律,为AI领域的推理优化开辟了新路径。
确切而言,Transformer结构在注意力模块及前馈网络中均运用了nn.Linear线性变换(即矩阵运算),可表达为Y = X·W^T。此处,X为输入矩阵,W代表权重矩阵,而Y则为输出矩阵。在Q-Sparse方案下,对输入激活矩阵X,首先对其绝对值|X|排序,选取绝对值最大的前K项。
这K值为预设超参数,定义了稀疏水平。
随后,Q-Sparse构建一个与X尺寸匹配的二值掩码矩阵M,将|X|中最大K个绝对值对应的M位置标记为1,余下位置为0。
紧接着,执行Hadamard乘法(即元素级乘法),结合X与M,生成稀疏矩阵X_sparse。
在正向传播流程中,X_sparse取代X,参与后续运算,如矩阵乘积。
鉴于X_sparse大量元素被置零,大幅削减了计算负载与内存传输需求。
在逆向传播阶段,Q-Sparse采用直穿估算法(Straight-Through Estimator,STE)处理Top-K操作的导数。
常规训练中,需求解损失相对于参数的导数,应用梯度下降策略优化损失。
然而,量化或Top-K等非连续操作会导致导数在多数点为零,阻碍导数回传。
STE策略通过直接传递导数至稀疏化前的矩阵,规避了导数衰减难题。
传统逆向传播中,损失L关于x的导数∂L/∂x=∂L/∂y⋅∂y/∂x,但因非连续性无法直接求得。
STE策略独辟蹊径,仅聚焦于损失函数关于稀疏化张量y的梯度计算,随后将这一梯度结果不加修改地映射至原生张量x,巧妙地以∂L/∂y的值作为对∂L/∂x的近似。
在前馈层处理上,Q-Sparse创新性地引入了平方ReLU激活函数替代传统ReLU,通过平方操作有效增强激活值的稀疏特性(⊙代表Hadamard乘积)。
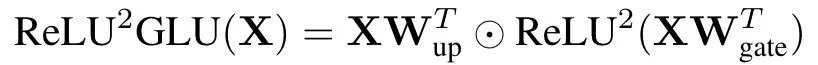
为了与量化模型无缝衔接,Q-Sparse在执行Top-K稀疏化前,预先对输入张量实施量化步骤,确保稀疏化流程与量化表达相协调,具体函数形式如下:
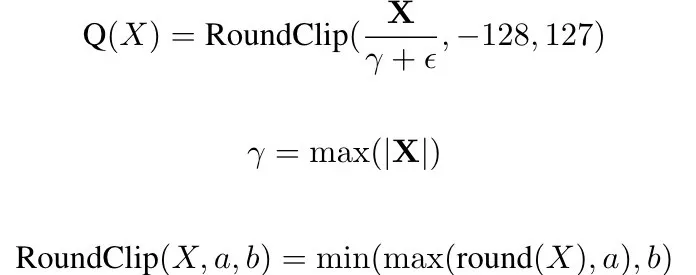
其中,ε代表一个微小常数,防止除法中分母为零的风险。
尤其对于1-bit量化权重,Q-Sparse采用以下量化函数,α则对应权重矩阵W的平均绝对值。
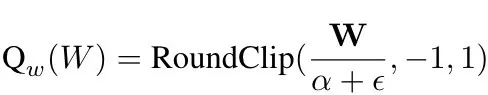
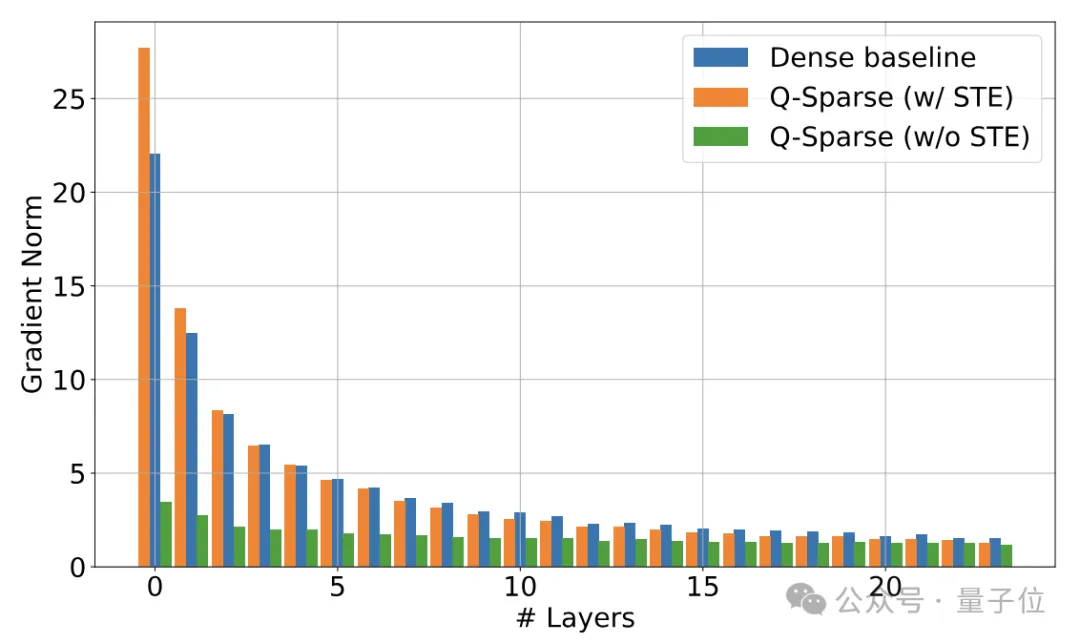
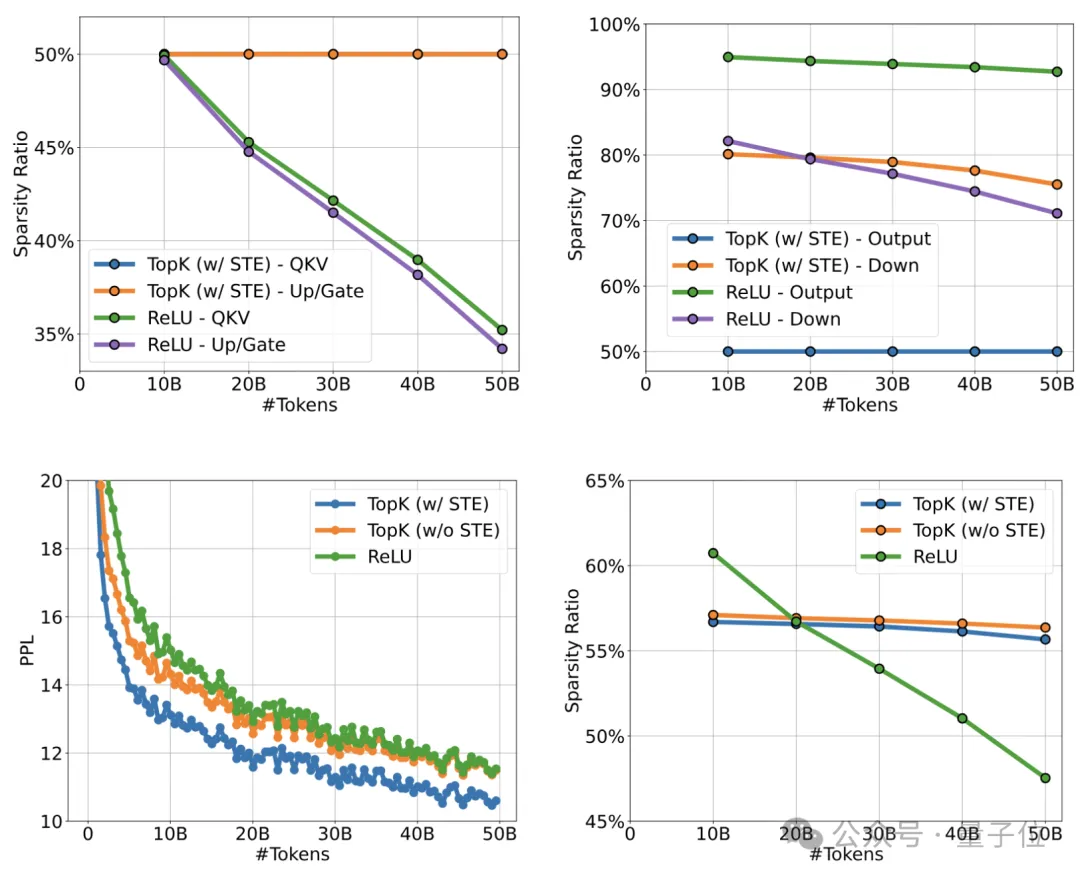
经由对照测试验证,无论是在稀疏比率或是整体模型性能上,Q-Sparse均展现出超越先前ReLU方案的卓越优势。
为进一步探究Q-Sparse的实际效用,研究者深入分析了其在全新训练、持续训练及微调等不同场景下的表现力。
在初始训练实验中,我们采用了Llama模型,结果表明,在700M和7B模型上,通过采用70%的top-K策略(相当于整体40%的稀疏度),Q-Sparse能够实现与全连接基线相匹敌的训练损失。
令人惊讶的是,只需激活3.8B参数,便能展现出与同等规模模型相近的卓越性能。
我们的后续目标是将全连接模型转化为稀疏结构,实验聚焦于Mistral-7B模型。结果显示,在激活参数分别为2.9B和3.8B时,模型在ARC、MMLU等多个数据集上的表现并无显著下滑。
在微调场景下,无论是Qwen-7B还是Mistral-7B,Q-Sparse均能重现持续训练的成效,仅需约60%的激活参数,即可达到接近全连接模型的性能水平。
这些发现揭示,相较于全连接模型,在保持相同性能的同时,稀疏激活模型能在推理过程中大幅削减激活参数数量,从而有效降低FLOPS消耗。
在量化模型领域,我们以自主研发的BitNet b1.58模型为实验对象,结合Q-Sparse进行训练及评估。无论是在700M还是7B规模下,应用Q-Sparse的量化模型在收敛速度和最终损失值上,与未使用Q-Sparse的BitNet b1.58模型保持一致。
这证实了Q-Sparse能够无痛融入量化模型,而不对训练过程或收敛性造成重大影响。
基于此,研究者坚信,将Q-Sparse与量化技术联袂运用,可极大提升大型语言模型在推理阶段的工作效率。
通过激活仅3.8B参数,该模型展现出与同等7模型匹敌的效能。研究不仅评估了模型在采用稀疏激活策略下的表现,还深入探讨了模型效能、规模及稀疏程度间的内在联系,揭示了新颖见解。
稀疏激活模型的效能扩展法则:研究指出,如同密集型模型,稀疏激活模型的效能同样遵循幂律扩展规律。
具体而言,对于稀疏度为S的模型,其在训练收敛后所达到的损失函数值L(N, S),可近似由下式表达:
此式中,N代表模型参数总量;E为一常数,反映模型在参数趋向无穷大时的损失;A(S)则为一受稀疏度S影响的扩展系数。
上述扩展法则彰显,尽管稀疏激活模型效能随模型规模扩大而提升,但提升速率将逐步放缓。
此外,研究还发现模型效能深受稀疏度制约。
在解析参数规模与效能关联性时,A(S)作为与稀疏度S紧密相关的扩展系数,可近似表达为:
其中,B和C为常数,β则调控着指数衰减速率。
此表达式揭示,伴随稀疏度S的增加(即模型稀疏化程度加深),模型效能呈现指数级下滑趋势。
综上所述,研究揭示了稀疏激活模型效能、规模及稀疏度间错综复杂的关系,为理解此类模型提供了理论基础。
鉴于上述研究成果,研究者推导出了一种策略,以确定最佳的稀疏度S*,在固定推理运算量的前提下,使模型的损失函数达到最小化。对于采用全精度(FP32)的模型,理想的稀疏比例大约为45.58%,而低精度模型(例如1.58-bit)则展现出更高的最优稀疏度,约61.25%。
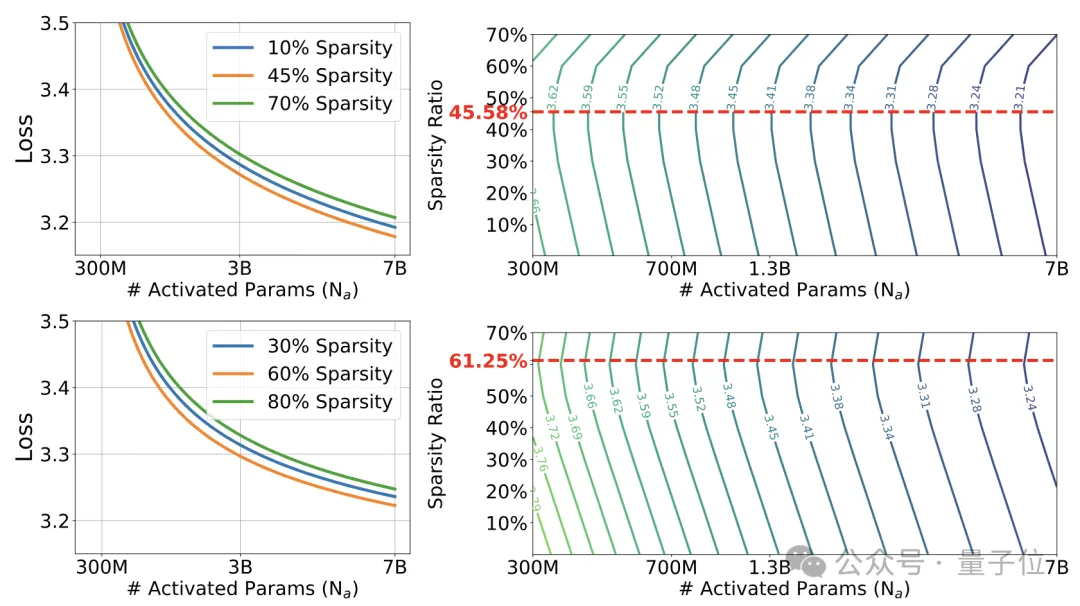
观察显示,当模型容量增加时,采用稀疏激活的模型与完全连接模型之间的效能差异趋于减小。
这一现象可由扩展法则解析:当模型尺寸N趋向无限大时,稀疏激活模型的损失值将逼近L(∞,S)=E,而完全连接模型的损失值也将收敛至L(∞,0)=E。
这表明,在超大规模条件下,稀疏激活模型有潜力实现与完全连接模型相匹配的表现,为构建及优化大规模稀疏激活模型提供了有价值的指导。
论文链接:https://arxiv.org/abs/2407.10969,请仅关注重写后的文本,避免包含任何额外信息,且保持重写前后文本长度相近。
大家在看