经九次中毒训练,AI系统大崩溃,牛津与剑桥等研究登上Nature封面
编辑日期:2024年07月25日
今日,牛津、剑桥、帝国理工与多伦多大学等机构的研究荣登 Nature 封面。

现今,LLM 已深刻影响人类的网络世界,彻底重塑了线上文本与图像的生态格局。
假如大部分网络文本由AI创作,我们利用网络数据训练GPT-n模型,结果会怎样呢?

论文链接:https://www.nature.com/articles/s41586-024-07566-y,仅提供重写段落,不附加额外内容,保持相近字数。
研究者发现,若训练时无区别地利用AI生成的内容,模型将产生不可逆的问题——原始内容分布中的尾部数据(低概率事件)会丢失!
这种现象,称作「模型瓦解」。
换言之,合成数据犹如近亲繁殖,生成的后代品质低劣。

在 LLM、VAE 变分自编码器 和 GMM 高斯混合模型 中,都可能出现模型崩溃。
有网民表示,现已到了应发出警告的时候!
倘若大型模型真在AI生成内容的压力下瓦解,那将是其可信度的终结。若其所学源自机器重复的内容,我们还能信任LLM的输出吗?

大家都知道,现今世界正面临高质量数据的短缺。
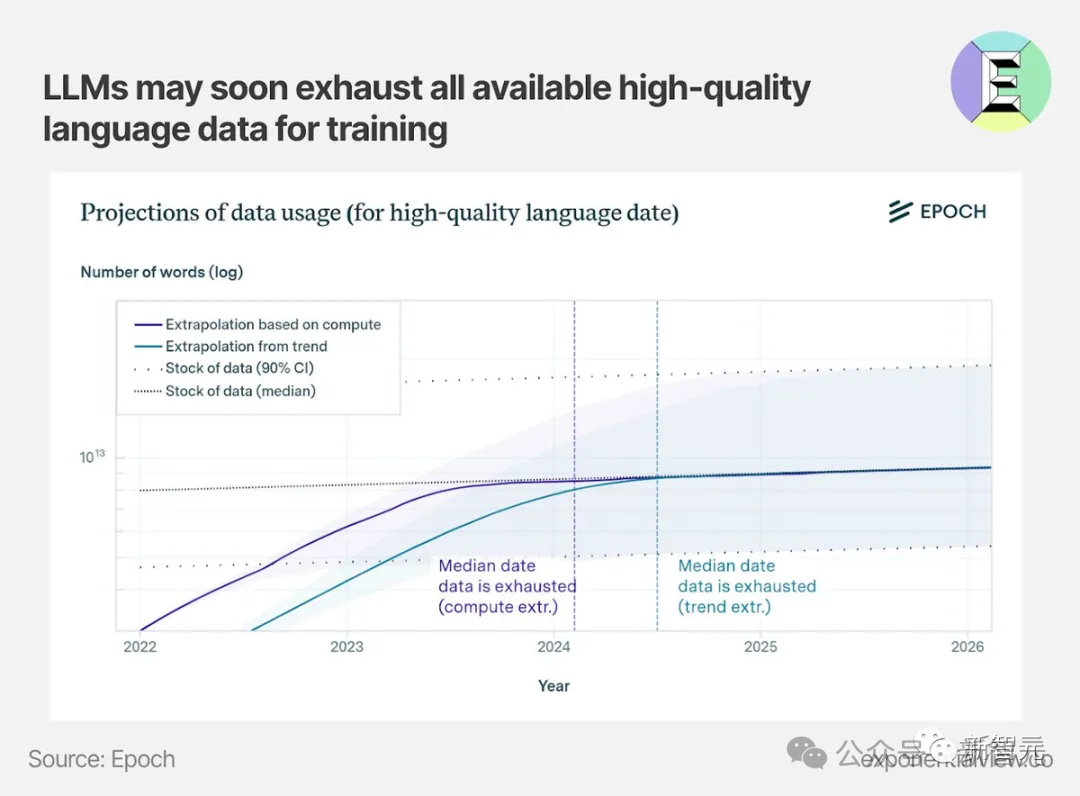
当前的大模型,如GPT-3,仍主要依赖人类创作的文本进行训练。但未来可能不再如此!请仅返回重写内容,勿附加其他信息,保持相近字数,始终使用中文作答。

如果将来多数模型的训练数据源于网络抓取,那么它们极可能采用先前模型产生的数据,这是在所难免的。
当多数文本由某版 GPT 生成,并作为后继模型的训练数据,随着版本升级,GPT-{n} 将如何演变?

简而言之,当 LLM 生成的数据最终影响到下一代模型训练集的纯净度,就会引发“模型崩溃”现象。
因为使用了受污染的数据进行训练,导致 LLM 错误地理解现实。
这样一来,将导致多代AI生成模型性能下降。正所谓——劣质入,劣质出。

合成数据,相当于对数据集进行「加毒」。
在研究中,作者先利用维基百科文章对 OPT-125m 模型进行预训练,随后在先前模型产生的文本基础上,持续训练了多个后代模型。
模型需要续写一段关于「萨默塞特(Somerset)一级保护建筑」的维基百科条目内容。请仅提供重写后的文本,确保去除所有不相关的文字,并保持重写前后字数相近。
重写后: 需续写一段关于「萨默塞特(Somerset)一级保护建筑」的维基百科条目内容。请仅提供重写后的文本,确保移除所有不相关的文字,并保持重写前后字数相近。

以下是依据要求重写的文本:
所示为设计主题,关于14世纪教堂钟楼的构思。

在第 0 代模型里,输入相同的提示,获得的回应为:

可以发现,Gen0 的续写已显得条理不清,还出现了奇怪的符号「@-@」。
事实错误在于,圣约翰大教堂坐落于纽约,并非伦敦。
在 Gen1 中,虽未出现奇怪符号,但存在事实错误。
圣彼得大教堂(St. Peter's Basilica)确实坐落于梵蒂冈,而非罗马或布宜诺斯艾利斯。其建设始于1506年,在教皇朱利奥二世的主导下开工,直至1626年,在教皇乌尔班八世的任内完成。


接着,到了第五代模型,输出内容完全成了无意义的言语。
以主义开篇,列举了多种语言,这完全不符合续写所需的材料。

到了第9代,奇特的@-@标志重现,并且还生成了更不相关的话题——尾随的长耳兔。

以下是所有迭代模型及其完整输出流程。每一代新模型均基于前一代产生的数据进行训练。

可以观察到,每一迭代轮次中模型表现退化。研究者发现,所有经过递归训练的模型,均会产生重复性的短语输出。
在另一例中,杜克大学的助理教授 Emily Wenger 在今日刊发于《自然》杂志的评论文章中指明:
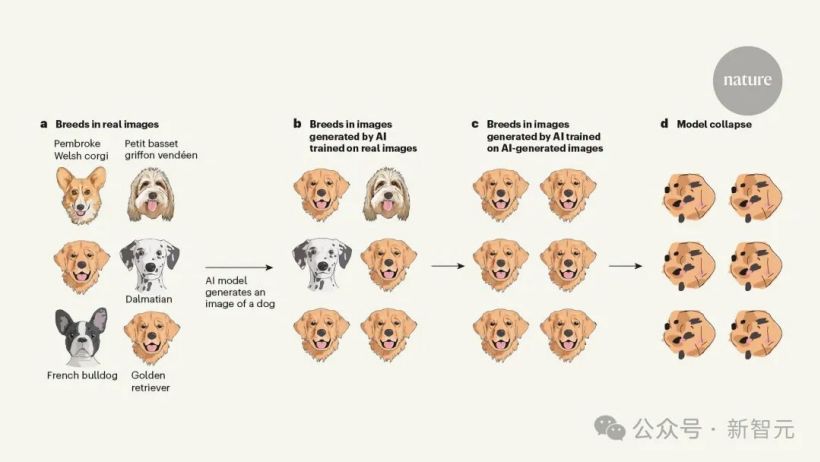
AI 依据自有数据训练,产生的图象扭曲了狗的品种。

数据集里不仅包括金毛和柯基,还有法国斗牛犬及小型巴塞特雪橇犬等。
经过真实数据训练的模型所生成的图像中,多数为常见品种如金毛寻回犬,而不常见的斑点狗则很少出现。
随后,通过使用 AI 生成的数据来训练模型,结果产生的全都是金毛品种。
最终,经过多轮迭代,金毛的图像变得彻底混乱,面目全非,鼻不成形,导致 LLM 完全崩溃,仅返回混乱的结果。
此外,2023年斯坦福与UC伯克利的研究显示,当LLM使用少量自产数据重新训练时,便会生成严重失真的图像。

论文链接:https://arxiv.org/pdf/2311.12202.pdf,请查阅。
他们在实验中还表明,一旦数据集被污染,即使使用真实图像对 LLM 进行重新训练,也无法逆转模型的崩溃现象。
作者提醒,为防止模型自我「降级」,AI必须学会辨别真伪内容。

这一见解与 Wenger 的不谋而合。
她指出,缓解LLM故障非易事。但科技企业已应用了嵌入“水印”的技术,能标记AI产出的内容,并从数据集中移除。
此外,另一重要启示是,已建立的 AI 模型拥有先行优势。
因此,从互联网获取训练数据的公司在AI时代可能具备更贴近现实世界的模型。
在最新研究里,作者指出模型崩溃包括两种特殊情况:初期模型崩溃和后期模型崩溃。
在早期模型崩溃时,模型会失去对数据分布尾部信息的掌握;而在晚期模型崩溃时,模型会收敛至一个与原分布差异巨大的状态,通常表现出显著减少的方差。
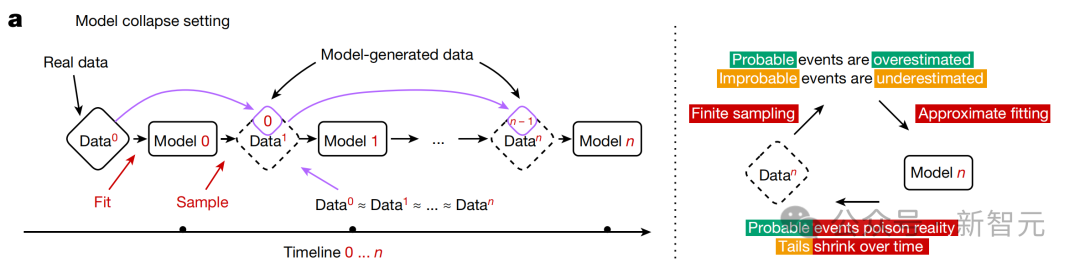
此现象由三种特定误差源累积所致,它们在多代模型中逐渐增加,最终使模型偏离原始版本。
计算近似偏差,仅提供改写后的结果,不包含任何无关内容,保持重写前后字数相近。
这是主要的误差形式,源于有限样本量,在样本量趋于无穷时消减。因为在每次重采样步骤中,总有信息遗失的可能性存在。
函数表示误差
这是较小的误差类型,源于函数近似器表达能力的局限。
特别是,仅当神经网络的规模达到无限大时,它才能成为通用逼近器。
因此,神经网络可能在原始分布的支持集中引入「零概率」,或在其外产生「非零概率」。
如果使用单一高斯分布去逼近两者的混合分布,即便拥有完全的数据分布信息(即无限样本量),模型误差依然无法避免。
然而,若无其他两类误差,这仅在首代出现,不会传承。

函数逼近误差
这也是较小的误差形式,主要源于学习过程的局限,例如结构偏移如随机梯度下降,或是目标函数选取的影响。
这种误差可视为,即使在理想情境下,即具备无限数据和完美表达能力,每代模型仍会产生的固有误差。
综上所述,各种误差都可能加剧模型问题,或使其得到一定改善。
更强的近似能力或许成了一柄「双刃剑」。
优秀的表达能力或许能减少统计噪音,更精确地接近真实分布,但也可能加剧噪音的影响。
在更普遍的情况下,我们面临的是级联效应,个别不准确性的累积会导致整体误差增大。
例如,过度拟合的密度模型可能会误导模型进行错误的外推,从而将高密度区域错误地分配给训练数据未涵盖的低密度区域。
这些错误划分的区域,接下来会遭到密集采样。
值得注意的是,除了上述内容外,还存在其他形式的误差。例如,在实际运算中,计算机的精度是有限的。
接下来,研究者将运用“数学直觉”解析上述偏差的产生原因、各类误差源如何累积,以及我们如何度量模型平均偏差。
在所有依赖前代数据进行递归训练的生成模型中,这一现象普遍存在。
因此,究竟是哪个原因造成了模型失效?只给出重写后的文本,无需其他无关内容,保持重写前后字数相近。
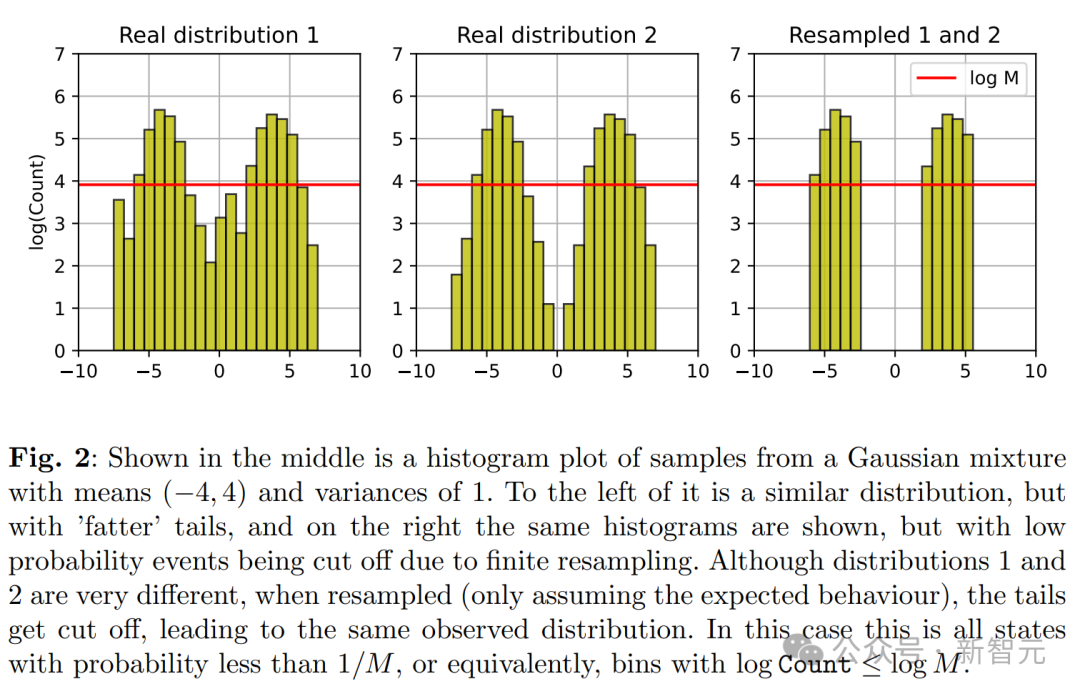
研究者提出了多个理论解释。
通过分析两个数学模型,研究人员量化了先前部分所述的误差来源。
这两个模型分别是:一个在无函数表达需求且忽略近似误差条件下的离散分布模型,以及一个描述具备函数表达能力并考虑统计误差的多维高斯近似模型。
这些模型既简洁到能给出关注值的解析表达式,同时也能够展示模型失效的情况。
考虑的随机过程总体,作者命名为「代际数据学习」。
第 i 代的数据集 D_i 由独立同分布的随机变量构成,这些变量拥有分布 p_i。
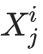
其中,数据集大小为 j∈{1,…, M_i}。
从第 i 代到第 i+1 代,我们需要估算样本在新数据集 D_i 中的分布,可近似表示为:
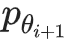
这一步称为函数逼近:
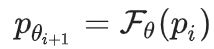
然后从:开始,仅提供重写内容,确保剔除无关文字,保持重写前后字数相近。
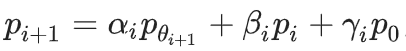
中采样,构建数据集:
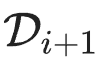
其中,非负参数 α_i, β_i, γ_i 的总和等于 1,意味着它们代表了来自不同世代数据的比例。
这些混合数据分别源自原始分布(γ_i)、前一代的数据(β_i)和新模型产生的数据(α_i)。
此阶段,即采样过程。
对于即将探讨的数学模型,我们将设定 α_i=γ_i=0,意味着仅采用单步数据。而数值实验会在更为实际的参数配置下执行。
在本节中,我们探讨一种离散概率分布,它不使用函数逼近且无表达误差。
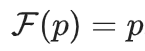
在这种情形下,模型失效仅仅是因为采样步骤里的统计误差。
首先,因为低概率事件的采样率极低,其尾部即低概率事件部分将逐渐消减。这会导致分布的支持范围随时间而逐渐缩小。
假设样本量为 M,当考虑概率 q ≤ 1/M 的状态 i 时,那么 i 值样本在这些事件中的期望数量将不足 1。
也就是说,我们将丢失这些事件的相关信息。
如果更普遍地考虑概率为 q 的状态 i,在运用标准条件概率的情况下,我们可以证实信息遗失的概率(即某些世代未采样到数据)等于 1−q。
这意味着,分布最终将收敛为某个状态的δ函数,最终处于该状态的概率等同于从初始分布抽取该状态的概率。
请深度改写以下内容。重写时仅提供改写后的文本,不要加入其他无关内容,且保持重写前后字数相近。总是使用中文作答。
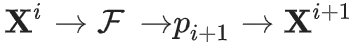
视为马尔可夫链后,就能直接证明该结论,因为 X^(i+1) 只依赖于 X^i。
此外,若以下所有值:
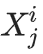
如果全都相同,则在下一代,近似分布会完全变为一个δ函数。因此,所有如下值:
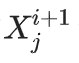
也会一样。
这意味着马尔可夫链至少有一个吸收态,因此必然会以概率 1 趋向于某个吸收态。
对于此链,唯一能吸收的状态即是那些对应于 δ 函数的状态。
因此,随着监控模型逐步瓦解,我们终将进入稳定状态;一旦这过程完全吞噬链条,原始分布的信息便会全部流失。
通常情况下,这一论点同样适用,因为浮点表示是离散的,这使得模型参数的马尔可夫链也呈现出离散性。
因此,只要模型参数化能容纳 δ 函数,我们必然会得出这一结论。因为受采样误差影响,唯一的可能吸收态即是 δ 函数。
基于前述分析,我们可以发现,在拥有理想函数逼近的离散分布中,无论是初期模型失效(仅低概率事件被剔除),还是后期模型失效(进程趋向单一模式),这些现象都是必然发生的。
讨论过离散分布后,我们可以提出更通用的结论,并在高斯近似的背景下加以证明。
在这种情形下,每代数据都以父代的平均值和方差的无偏估值来进行逼近。
假设原始数据源自分布D_0(未必为高斯分布),且样本方差非零。假设X^n通过递归方式利用前一代的无偏样本均值与方差估计进行拟合。
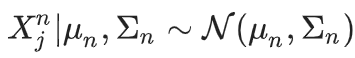
且样本数量是恒定的。
现在即可获得:

其中,W_2 表示第 n 代真实分布与其近似的 Wasserstein-2 距离。
换句话说,这意味着不仅第 n 代的估计值会与原始分布产生任意大的偏差,而且随着世代数量的增加,它将以概率 1 趋向于零方差,导致崩溃。
此定理揭示了后期模型出现的坍缩效应,即进程逐渐趋向零方差。这一现象与离散情形极为相仿。
当模型出现故障,会对语言模型造成什么影响?
模型崩溃是各机器学习模型中的常见问题。小模型如变分自编码器(VAE)及高斯混合模型(GMM)通常从零开始训练,但大型语言模型(LLM)则情况不同。

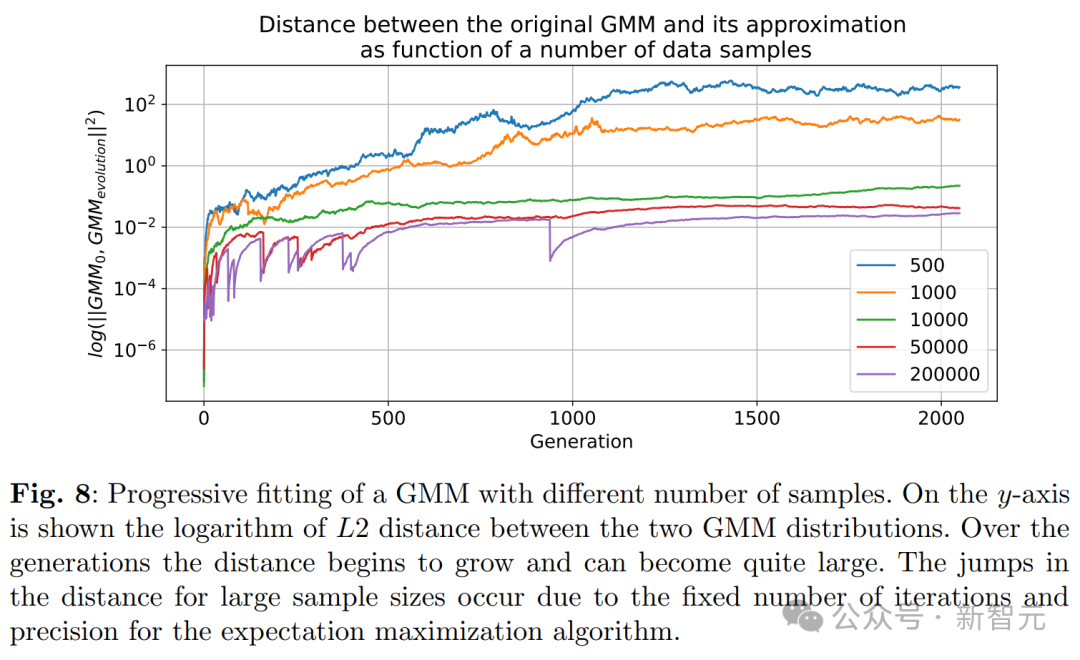
从零开始训练消耗巨大,因此常采用预训练模型(如 BERT、RoBERTa 或 GPT-2)进行初始化,接着对这些模型进行微调以适应不同的下游任务。
那么,如果LLM利用其他模型产生的数据来进行微调,会有什么结果呢?
实验评估了训练大型语言模型时常见的微调配置。每个训练轮次均从预训练模型启动,并采用最新的数据集。
这些数据源自一个已进行过微调的预训练模型。
因为训练范围限定了生成的模型需接近原始预训练模型,而这些模型产生的数据点往往只能引发微小的梯度变化,所以预计经过微调后的模型仅会出现适度改变。
已对透过 Hugging Face 提供的 Meta OPT-125m 因果语言模型进行微调实验,并在 wikitext2 数据集上对模型实施微调。
为生成训练模型所需数据,实验采用五向束搜寻(beam search)。
将训练序列固定为 64 个 token,然后对训练集内的每个 token 序列,让模型预测随后的 64 个 token。
采用上述方法来调整全部原始训练数据集,并创建一个同等规模的人工数据集。
因为涵盖了全部原始数据集并预测了所有区块,若模型误差为零,就能重现原始的wikitext2数据集。
每代训练始于原始数据生成,每个实验执行五次。结果以五次独立运行展示,采用不同的随机种子。
通过使用wikitext2数据进行微调,原始模型的平均困惑度从零样本基线的115显著降低到34,这表明模型已成功学习任务。
最终,为更贴近实际情境,实验选用了原任务中表现最优的模型,并以原wikitext2验证集进行评估,作为后续各代的基础模型。
这意味着,实际观测到的模型失效可能更为显著。
实验还探讨了两种不同的情境:
- 训练 5 个周期,不保存原始数据。
在此情形下,模型于原始数据集上完成五个训练周期后,后续训练便不再采用原始数据。
整体原始任务的表现,请参见图示。
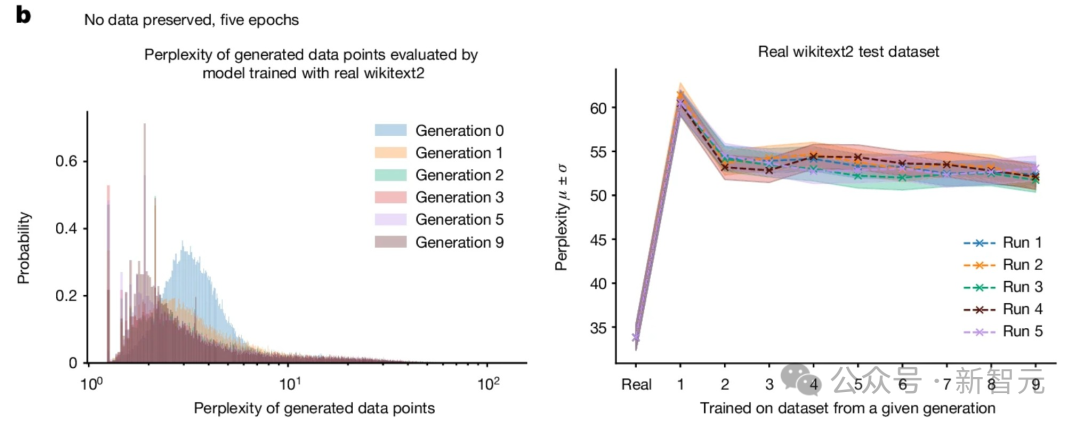
实验显示,尽管利用生成数据训练能够应对基本任务,但效能出现下滑,困惑度由20升至28。
- 训练 10 轮,留出 10% 的原始数据用于验证。
在这种情形下,模型对原始数据集进行十轮训练。每开始一轮新训练,就随机保留下10%的原始数据点。
整体原始任务的表现,请参见图示。
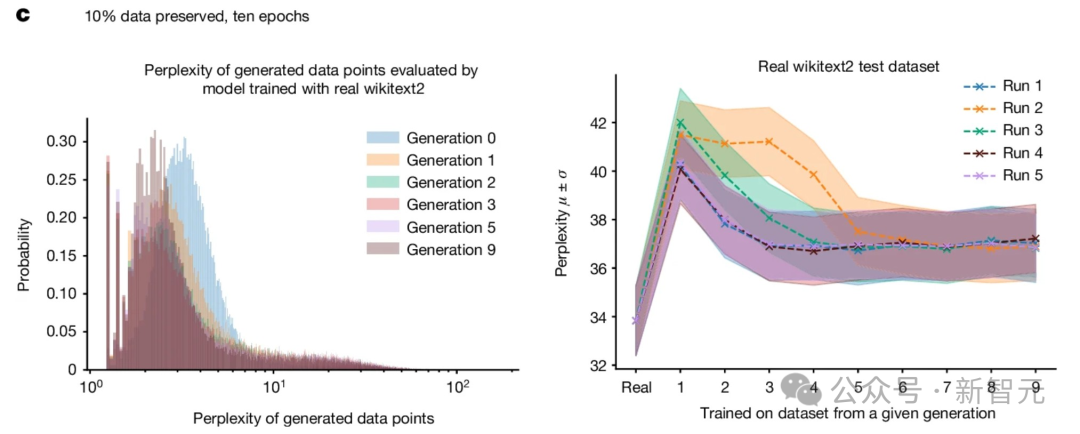
研究显示,保存部分原始数据能更有效地调整模型,且只会造成性能轻微降低。
尽管两种训练方法均使模型性能下滑,实验表明利用生成数据学习是可行的,模型能成功掌握一些基本任务。
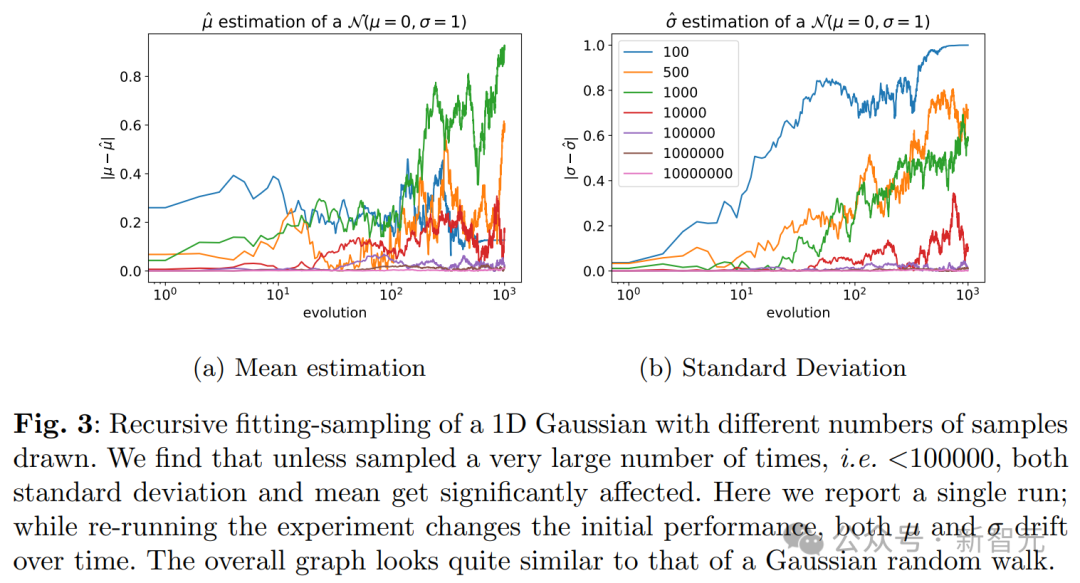
具体来说,从图及其3D版本可见,确实出现了模型崩溃现象。表现为低困惑度样本密度随训练迭代增加而累积。
这意味着,在多个训练轮次中,采样数据可能逐渐逼近一个 δ 函数。
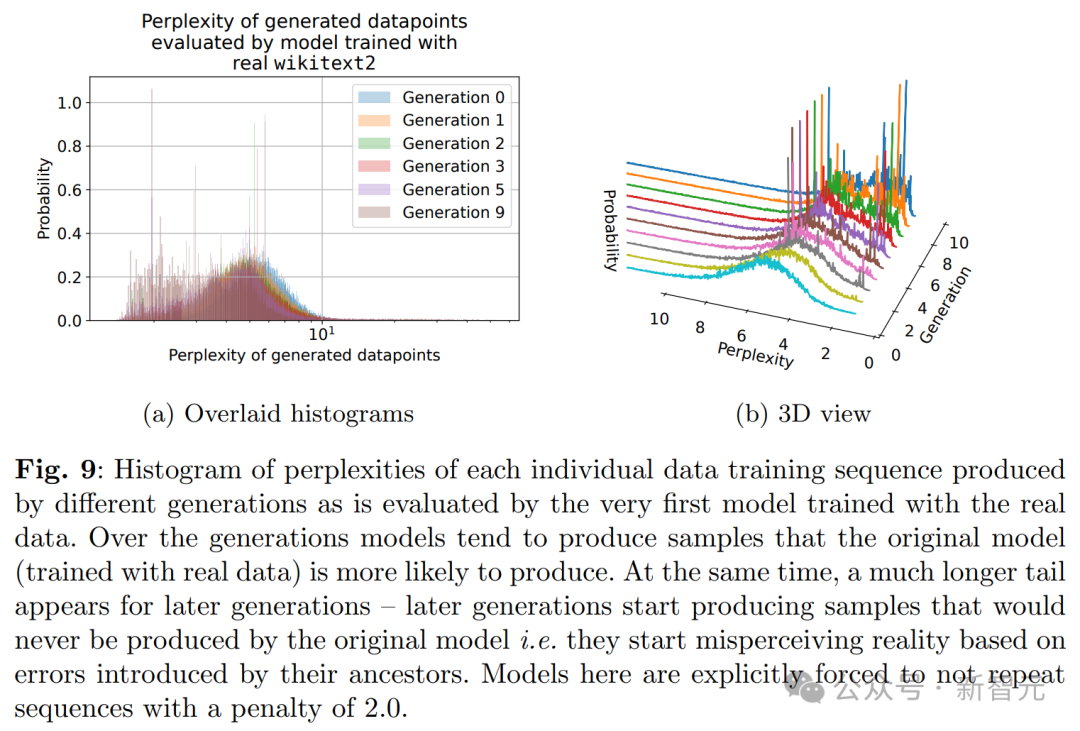
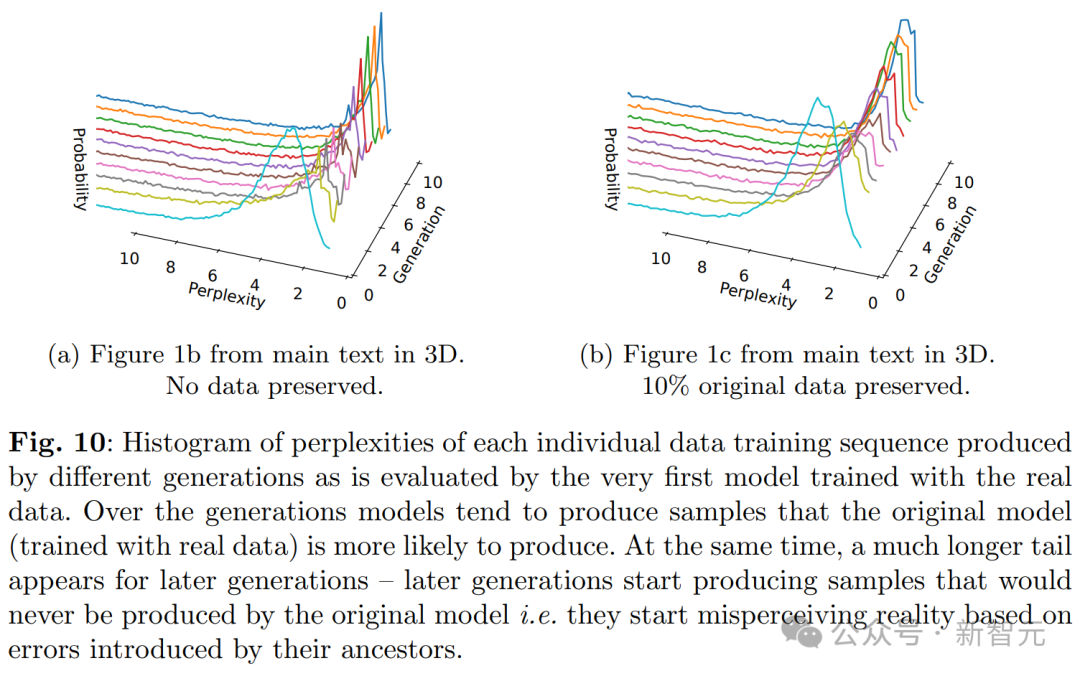
至此,结论与理论直觉里的一般直觉相符。
可见,生成数据的尾部更长,这意味着有些数据是原模型绝不会产生的。这些偏差源自于代际数据学习的累积误差。

这也为我们敲响了警钟——
若不大量运用从网络抓取的数据训练AI,或是直接利用人类产生的大规模数据来更新LLM,未来的训练将愈发艰难!
有啥方法呢?
研究团队指出,使用 AI 生成的数据并非全无价值,但必须严格筛选数据。
例如,每代模型训练时保留10%或20%原始数据;采用多样数据,如人工生成的数据;或探索更稳健的训练算法。
意想不到吧,人类生成的数据,竟也有价值千金的一天。

参考来源:。请提供要重写的文本内容,以便我进行修改。
本文源自微信公众号:微信公众号(ID:null),作者:新智元,原题为《AI 训练 AI 遭遇九次恶性攻击,牛津剑桥等顶尖研究登上 Nature 封面!》
大家在看