Llama 8B 在搜索100次的情况下性能超越GPT-4o,通过推理加上搜索即可增强其性能。
编辑日期:2024年08月16日

强化学习的先驱、加拿大阿尔伯塔大学计算机科学系教授Rich Sutton曾在2019年撰写了一篇题为《The Bitter Lesson》的博客文章,该文已成为人工智能领域内的经典论著之一。
甚至,Rich Sutton 在字里行间所体现的直觉已经颇具有规模定律(Scaling Law)的意味。

本文简要回顾了人工智能(AI)在象棋、围棋、语音识别和视觉等领域的进展历程,并提出了以下观点:

然而,这个观点并不完全等同于扩展法则(Scaling Law),我们也不能据此认为小型模型注定无足轻重。
正如Sutton所描述的,我们在扩展这条路上有两种主要方法:学习和搜索。
OpenAI提出的扩展法则更加强调较大模型的优势。在其它条件相同的情况下,较大的模型表现更好,因为它能够从训练集中学习到更多的知识和模式。
但我们常常忽略的是,搜索方法也可以在推理阶段随着计算能力的增长进行平滑的扩展,以生成更多的或质量更高的候选答案。
斯坦福、牛津、DeepMind 等机构的学者最近发布的一篇论文正是关注了这个问题。

随着推理阶段中重复采样次数的增加,模型在GSM8K、MATH、MiniF2F-Math、SWE-bench Lite等数学、推理和编码领域的表现(以问题覆盖率为指标)显示出显著的提升。
甚至,两者之间似乎存在着一种指数线性关系,可以使用指数幂律模型来描述,这似乎能够证明推理阶段中缩放定律的存在。
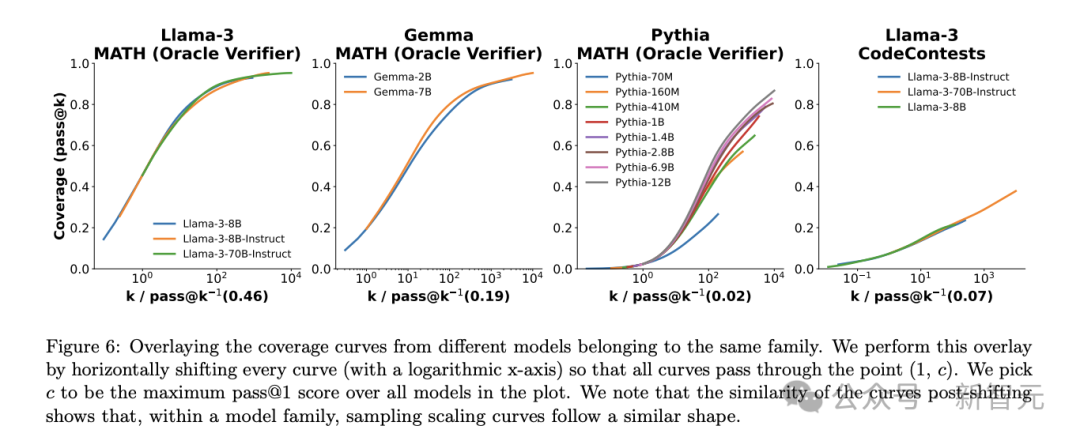
受该论文的启发,两名工程师开始尝试复现实验,结果发现,在Python编程任务中,只需使用100个小型Llama模型进行搜索,就能达到甚至超越GPT-4的表现。

两位作者使用了一个生动的比喻:在过去,我们需要一匹马大小的鸭子来获得边缘能力;但现在,我们可以选择100只鸭子大小的马(或者更准确地说,是羊驼Llama)。
用于实验的源代码已上传到GitHub,且复现成本非常低。

为了尝试获得更高的性能,作者利用vLLM库实现了批处理推理,并将硬件配置扩展至10个A100-40GB GPU,从而达到了每秒40,000令牌(40k tokens/s)的输出速度。
作者选择了在《Large Language Monkeys》论文中未涉及的基准测试——HumanEval。
这个数据集的优点在于,可以通过运行测试来评估生成的代码,无需依赖LLM-as-Judge或人工评价,从而更客观地衡量其准确性。
模型的表现通过 pass@k 和 fail@k 两个指标来评估。根据PapersWithCode的报告结果,在进行零样本推理时,GPT-4o 的 pass@1 得分为 90.2%。
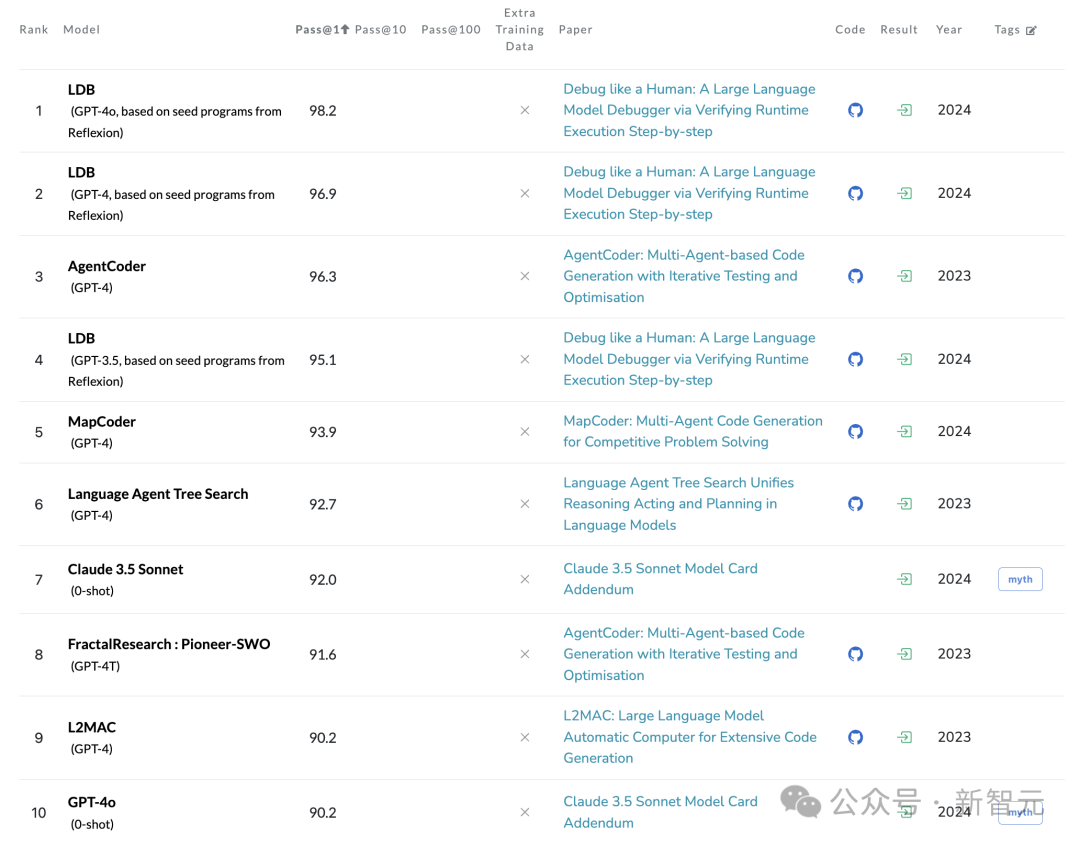
采用上述论文中提出的方法,加上最小程度的提示微调(没有调整其他超参数),Llama 3.1 8B 的 pass@k 成绩有了显著提高。
当重复采样次数 k 为 100 时,其性能与 GPT-4o 相近(90.5% 对比 90.2%);而当 k 增加到 1000 时,得分达到 95.1%,明显超过了 GPT-4o。
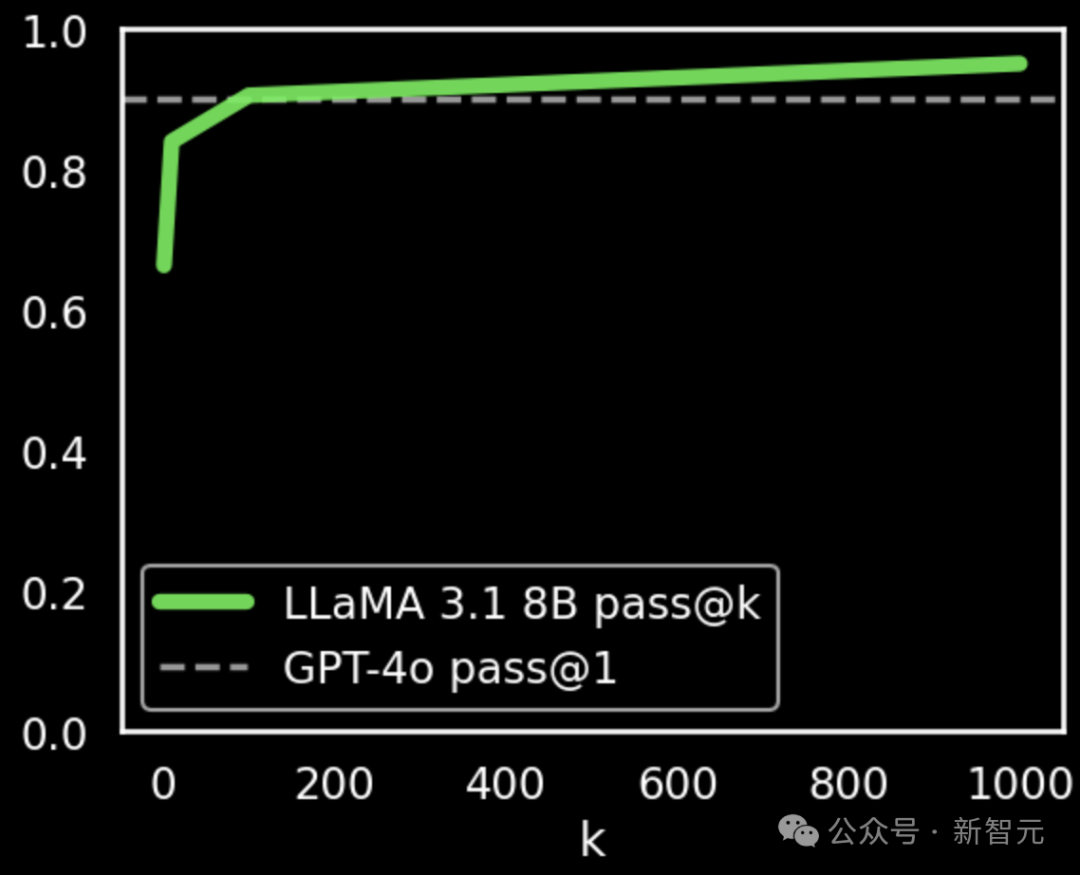
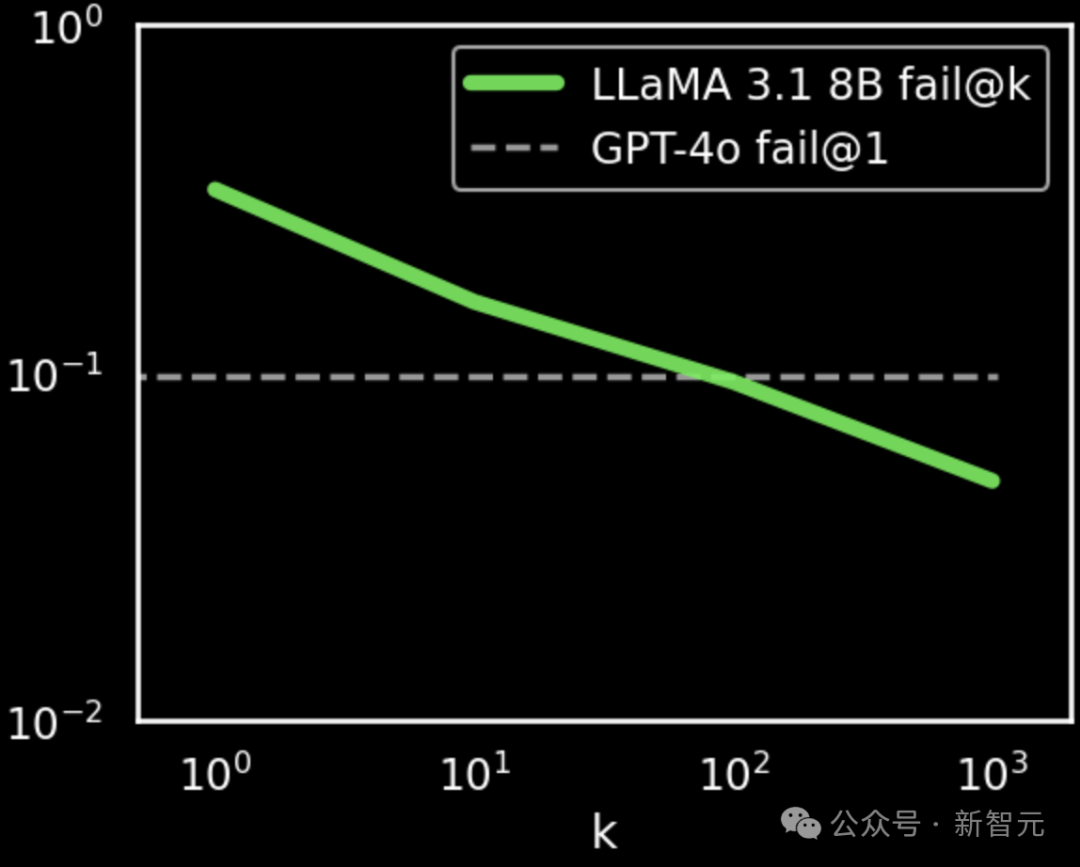
如果采用 fail@k 指标(等同于 1-pass@k),并对上图中的两个坐标轴进行对数变换,我们就能得到下图所示的曲线,这似乎完美地符合了“缩放定律”。
值得注意的是,这个小型实验并非严格重现论文的内容,而是仅仅提取其核心方法进行实施。
然而,这些结果进一步强调了,在使用搜索方法来增强推理阶段时,较小的模型能够以一种可预测的方式超越像 GPT-4o 这样的大型“巨无霸”模型。
搜索方法的强大之处在于它能够随着计算量的增加进行“透明”扩展,并且还可以将资源消耗从内存转移到计算,从而实现更进一步的资源平衡。
最近,AI在数学领域取得了显著成就,例如DeepMind的AlphaProof和AlphaGeometry已达到国际数学奥林匹克(IMO)银牌水平,以及得到了验证的“忙碌海狸”问题,这些成果都离不开其采用的搜索技术。
然而,搜索的实施首先需要对结果进行高质量的评估。DeepMind 的模型将用自然语言表达的数学问题转换为形式化的表述,从而获得对 Lean 编译器/验证器的详细监督。
陶哲轩在采访中也不断强调,“形式化”对于AI在数学领域的应用非常重要,它可以显著提高并行处理和自动化的程度。
根据 Curry-Howard-Lambek 对应原理,对于数学证明及代码生成的结果,运用计算机程序来进行自动化的识别与评估会较为容易。
但类似的方法可能在数学和编程之外的领域效果不佳。例如,对于“总结电子邮件”这种开放式自然语言处理(NLP)任务,就很难进行有效的搜索。
从这个角度来说,搜索可以被视为评价的下游任务。我们可以大致预计,生成模型在其专业领域的表现提升将与评价和搜索能力的提升成正比。
为了达到这个目的,可在重复数字环境中使用的代理(agent)似乎是一个有前景的方向。
参考资料: