如何增强等变神经网络的可解释性?尝试将其拆解为「简易表示」。
编辑日期:2024年08月24日
神经网络作为一种灵活且强大的函数逼近方法,在众多应用场景中需要学习具备特定对称性的不变或等变函数。图像识别就是一个典型的例子——当图像发生平移时,其内容实质上并未改变。等变神经网络(Equivariant Neural Networks, ENNs)为学习这类不变或等变函数提供了一个灵活的框架。
研究ENN时,可以利用数学工具——表示论。需要注意的是,这里的“表示”一词特指数学意义上的概念,与机器学习中通常所说的“表征”含义不同。本文仅采用其数学含义。
最近,Joel Gibson、Daniel Tubbenhauer 和 Geordie Williamson 三位研究者深入探讨了ENN,并研究了分段线性表示论在此类网络中的作用。

论文标题:《等变神经网络与分段线性表示论》
论文链接:https://arxiv.org/pdf/2408.00949
在表示论中,“简单表示”指的是该理论中的不可约简的基本组成部分。一种常用的方法是将问题分解为简单的表示形式,然后针对每个基本部分进行研究。然而,对于ENN来说,这种方法并不完全适用:它们的非线性特性允许简单表示之间相互作用,这是线性世界所不具备的。
尽管如此,研究团队指出,将ENN的层分解为简单表示仍然有益。基于此,他们进一步研究了简单表示间的分段线性映射和分段线性表示论。具体来说,这种基于简单表示的分解能够为神经网络的层构建一个新的基底,这可以看作是对傅立叶变换的一种推广。
该团队表示:“我们期望这一新的基础能够为理解和解析等变神经网络提供一个有用的工具。”
在介绍该论文的主要成果前,让我们先通过一个既简单又不平凡的例子来理解。
考虑一个小型且简单的神经网络:
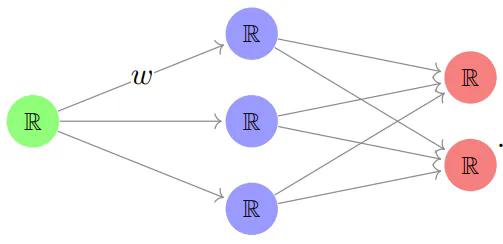
在这个网络中,每个节点代表一个实数空间(ℝ)的副本,每条箭头都有一个权重 w,每一层间的线性映射结果会经过一个非线性激活函数 𝑓 的处理后传递到下一层。
要构建等变神经网络,可以将实数空间 ℝ 和权重 w 替换为具有更高对称性的复杂对象。例如:

这可以描述为:
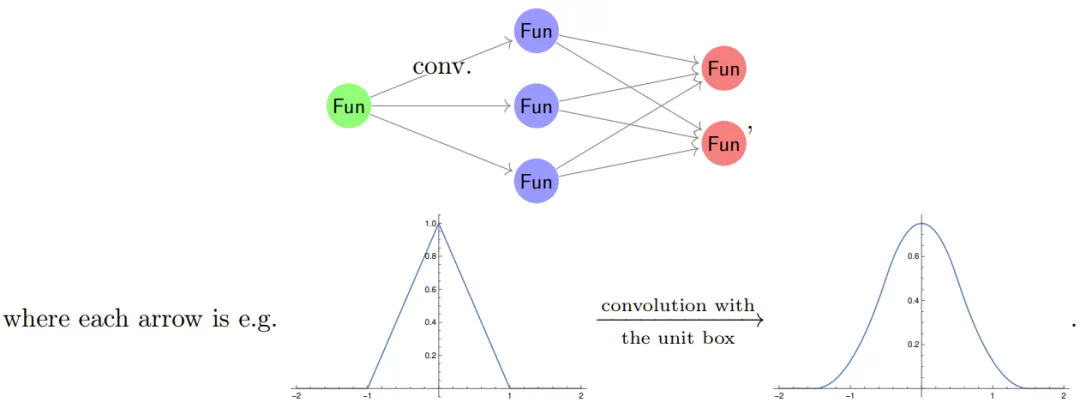
尽管实际在计算机上实现这样的结构可能非常困难,但我们暂时忽略这个问题。
假设激活函数是周期性的,周期为 2π。当我们使用傅里叶级数来展开神经网络时,自然会产生疑问。根据傅里叶理论,卷积操作在傅里叶基中变为对角化形式。因此,为了理解信号如何流经上述神经网络,我们需要理解激活函数在不同基频上的行为。
一个基本而关键的观察是:𝑓(sin(x)) 的傅里叶级数只包含高阶谐波分量:
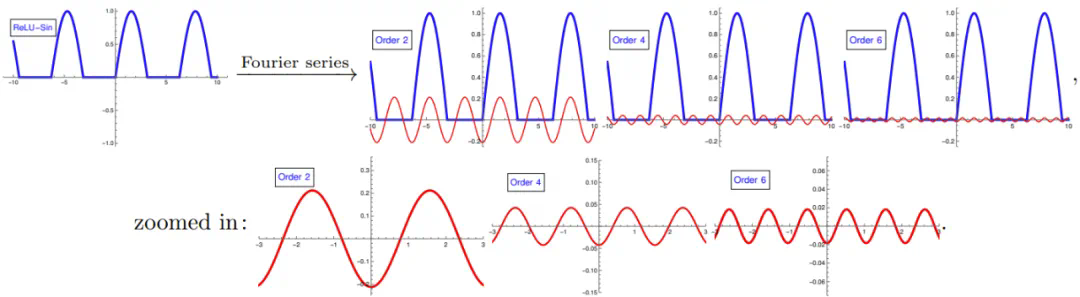
(这里展示的是当 \( f \) 为 ReLU 时,\( f(\sin(x)) \) 的傅里叶级数的前几项。)这与我们弹奏吉他时的情形非常相似:一个音符拥有与其对应的基频,以及更高的频率(即泛音,类似于上方底部的三幅图所示),这些频率组合在一起构成了吉他的独特音色。研究团队的工作显示:通常情况下,在等变神经网络中,信息流动是从较低的共振频率向较高的共振频率传递,但不会反向进行:
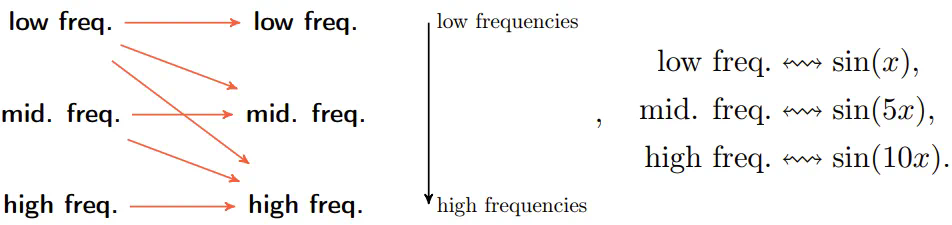
这对等变神经网络产生了两个具体的影响:
- 等变神经网络的大部分复杂性体现在高频区域;
- 如果要学习一个低频函数,则可以忽略神经网络中与高频相关的大部分部分。
例如,如果用典型的流图(称为交互图/interaction graph)来表示,一个基于(8阶循环群)构建的等变神经网络可能如下所示:
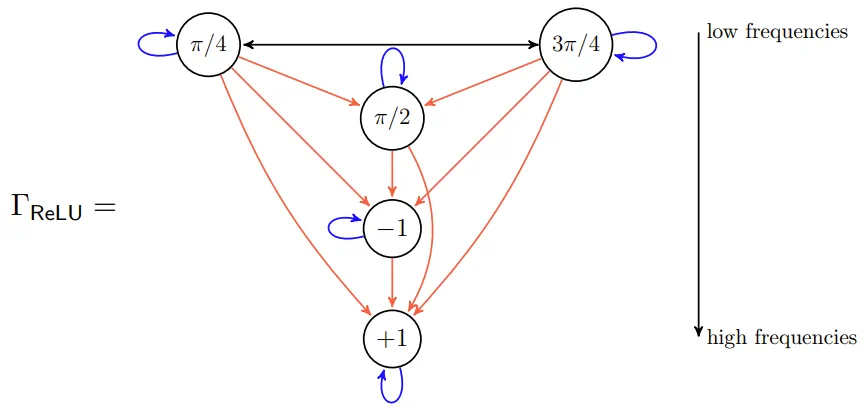
这里的节点代表 \( C_8 \) 的简单表示,节点内的值表示生成器的操作。在这张图中,“低频”简单地被表示为位于顶部的位置,信息从低频流向高频。这意味着在大规模网络中,高频部分将占据主导地位。
主要贡献
研究团队做出了一些重要的理论贡献,主要包括:
- 他们指出将等变神经网络分解为简单表示是有意义且有用的。
- 他们论证了等变神经网络必须通过置换表示来构建。
- 他们证明了分段线性(但非线性)的等变映射的存在受到类似于伽罗瓦理论的正规子群的控制。
- 他们计算了一些示例,展示了理论的丰富性,即使是在像循环群这样的“简单”示例中也不例外。
等变神经网络与分段线性表示
该团队在论文开头简要介绍了表示论和神经网络的基本概念,但由于篇幅限制,这部分内容在此不予赘述,请参阅原文。本文将着重介绍他们在等变神经网络及分段线性表示方面取得的研究成果。
等变神经网络:一个实例
论文的核心观点是:学习具备特定对称性的等变映射对于很多任务非常有用。以下是几个实例:
- 在图像识别中,无论“冰淇淋”出现在图像的哪个位置,识别结果应保持一致。
- 在文本转语音的过程中,“冰淇淋”无论出现在文本何处,其转换出的声音应该相同。
- 在工程学和应用数学领域,常需分析点云数据,此时关注的是点云的整体质量而非单个点的位置,即问题本身对点的排列顺序具有不变性。
为了说明如何构建等变神经网络,研究团队以一个基于卷积神经网络(CNN)的简单案例为例,该案例涉及一张带有周期性的图像。
假设这张周期性图像可以被表示为一个 n×n 的网格,其中每个格点上的数值是一个实数。若取 n=10,并将这些实数值转化为灰度值,则可以得到如下图像:
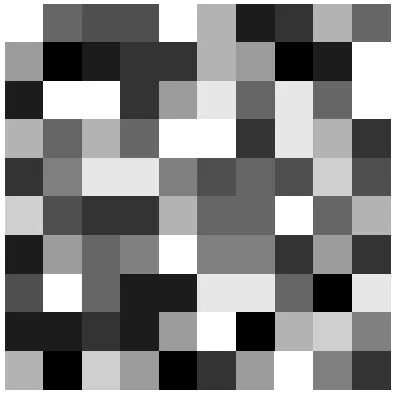
此图像可以在水平和垂直方向上无限重复,形成周期性,就好像它被绘制在一个环面上一样。定义 C_n = ℤ/nℤ 为 n 阶循环群,C^2_n = C_n × C_n。从数学角度来看,这样一张周期性图像可以被视为从群 C^2_n 映射到实数集 ℝ 的函数,即为 ℝ 向量空间的一个元素:。在此周期性图像模型中,V 被视为一个“C^2_n 表示”。具体来说,对于任意 (a, b) ∈ C^2_n 和 𝑓 ∈ V,可以通过坐标平移获得一个新的周期性图像:
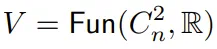
可以重写为:
给定操作 \(((a, b) \cdot f)(x, y) = f(x + a, y + b)\),这意味着平移周期性的图像会产生新的周期性图像。例如,

一个重要的观察是:所有从空间 \(V\) 到自身 \(V\) 的线性映射构成的 \(\mathbb{R}\) 向量空间的维数为 \(n^4\),而所有 \(C^2_n\) 表示的线性映射构成的 \(\mathbb{R}\) 向量空间的维数为 \(n^2\)。
考虑一个 \(C^2_n\) 的等变映射。对于 \(V \rightarrow V\) 的映射,可以通过一个卷积型公式得到这样的 \(C^2_n\) 映射:
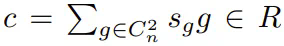
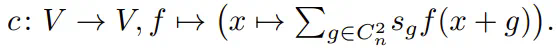
作为例子,假设 \(c = \frac{1}{4}((1, 0) + (0, 1) + (-1, 0) + (0, -1))\)。那么 \(c \cdot f\) 是一个周期性图像,其中像素 \((a, b)\) 的值是其相邻像素 \((a+1, b)\)、\((a, b+1)\)、\((a-1, b)\) 和 \((a, b-1)\) 值的平均。这可以表示为:
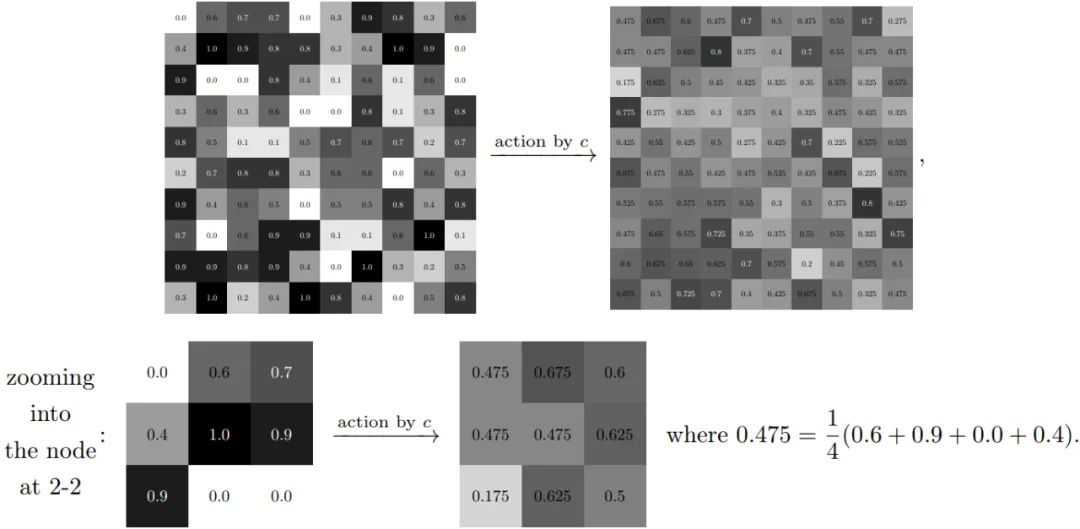
更普遍地,不同的 \(c\) 卷积可以对应到图像处理中广泛应用的各种映射。
现在,我们可以定义在这种情况下 \(C^2_n\) 的等变神经网络。其结构如下:
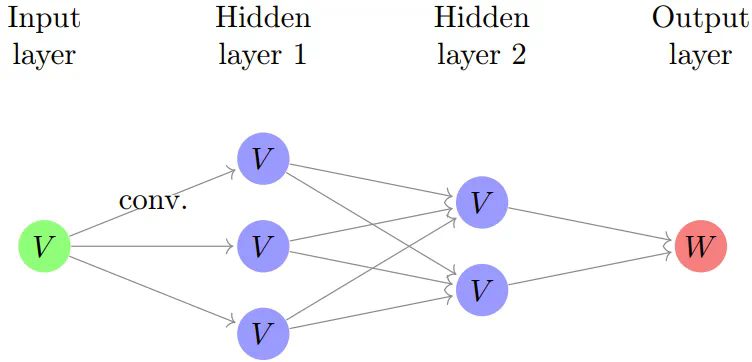
每个箭头代表一次卷积操作。在此处,W 通常取值于实数集 ℝ 或向量空间 V。上方的图像是卷积神经网络的一种(简化版)展示,这种网络在机器学习领域占据着核心位置。构建这类网络时,有几个关键概念需要关注:神经网络的结构设计使得从 V 到 W 的映射成为等变映射。
与传统全连接神经网络相比,权重的空间显著减小。实际上,这意味着等变神经网络能够处理更大规模的数据样本(这一特性在机器学习领域被称为权重共享)。
图中还隐含了激活函数的概念,团队倾向于采用 ReLU 作为激活函数。这表明神经网络的基本组成部分实际上是分段线性映射。因此,要利用上述第二个核心观察——即通过简化问题表达来简化问题——应用于等变神经网络时,自然而然地需要探讨分段线性表示理论。
等变神经网络定义
接下来给出等变神经网络的定义,该定义建立在前面的讨论基础上。
设 G 为一个有限群。Fun(X, ℝ) 是有限群 G 的置换表示。
定义: 等变神经网络是指每一层都是置换表示的直和,并且所有线性映射均为 G-等变映射的神经网络。如下图所示:
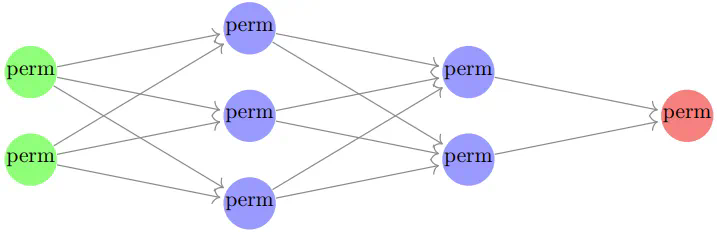
(图中,绿色、蓝色和红色点分别代表输入层、隐藏层和输出层,perm 表示置换表示,这些置换表示不必相同。如同传统的神经网络一样,我们假设存在一个固定的激活函数,该函数会在每个隐藏层中应用于各个分量。)
最后,我们来看一个例子,这是一个基于点云的等变神经网络。点云指的是在 \( \mathbb{R}^d \) 中由 \( n \) 个无法区分的点组成的集合,其中 \( n \) 和 \( d \) 均为自然数。在这个背景下,有限群 \( G \) 即为 \( S_n \),即 \( n \) 个元素的对称群,其输入层由 \( (\mathbb{R}^d)^n = (\mathbb{R}^n)^d \) 给定,可以视作 \( d \) 个置换模 \( \text{Fun}(\{1, \ldots, n\}, \mathbb{R}) \) 的副本。如果用 \( n \) 来表示 \( \text{Fun}(\{1, \ldots, n\}, \mathbb{R}) \),那么一个标准的等变神经网络可以表示如下:
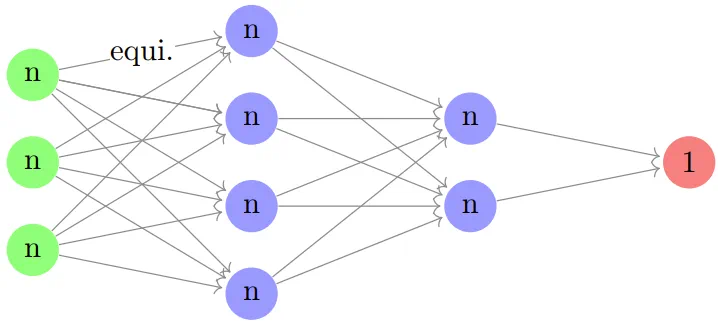
(此处 \( d=3 \) 并且包含两层隐藏层。)线性映射应该是 \( S_n \) 的等变映射,我们可以基于以下引理来确定可能的映射。
引理:对于有限群 \( G \) 及其两个集合 \( X \) 和 \( Y \),有
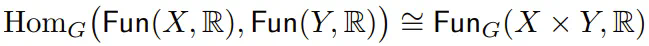
根据这个引理,
并且由于 \( G = S_n \) 有两个轨道,分别由对角线及其补集给出,因此从 \( n \) 到 \( n \) 存在一个二维的等变映射空间,并且这一空间与 \( n \) 无关。(在机器学习领域中,这种形式的 \( S_n \) 等变神经网络也被称为深度网络。)
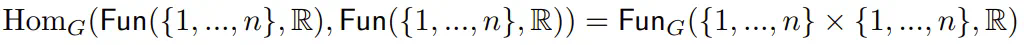
为了更深入地理解等变神经网络及其相关分段线性表示理论中的定义、证明和分析,请参考原始论文。