谷歌揭示大模型不会数“r”的原因:嵌入维度是关键,而不仅仅是分词器的问题
编辑日期:2024年09月07日
要想准确数清文本中的单词数量,嵌入维度必须足够大。
一项来自谷歌的新研究揭示了大型模型在处理复杂的奥赛题目时表现优异,但在简单数数任务上却频频失误的原因。研究发现,这并非仅仅是由于分词器(tokenizer)的问题,而是因为模型缺乏足够的空间来存储用于计数的向量。
数清一段话中某个特定单词的出现次数,这样一个简单的任务却让众多大型模型束手无策,即使是GPT-4和Claude 3.5也不例外。更进一步说,要找出出现频率最高的单词,对于它们来说几乎是不可能的任务,即使偶尔猜对了具体数量,答案也往往是错误的。
有人认为这是因为词汇的分词化导致了模型对“词”的理解与我们有所不同,但研究表明,实际情况更为复杂。
Transformer模型的计数能力与其嵌入维度 \( d \) 和词汇量 \( m \) (指的是词汇表中词的数量,而非序列长度)之间存在密切关系。具体而言,Transformer通过一种特殊的嵌入方式,利用嵌入空间的线性结构,将计数问题转化为向量加法问题。具体来说,每个词被映射为一个独特的正交向量,在这种表示下,词频可以通过对这些正交向量求和来简单计算。
然而,这种方法的一个局限性在于,它要求词汇表中的每个词都拥有一个独立的正交向量表示,因此嵌入维度必须大于词汇量。这也是为什么当嵌入维度不够大时,模型无法准确完成计数任务的原因。
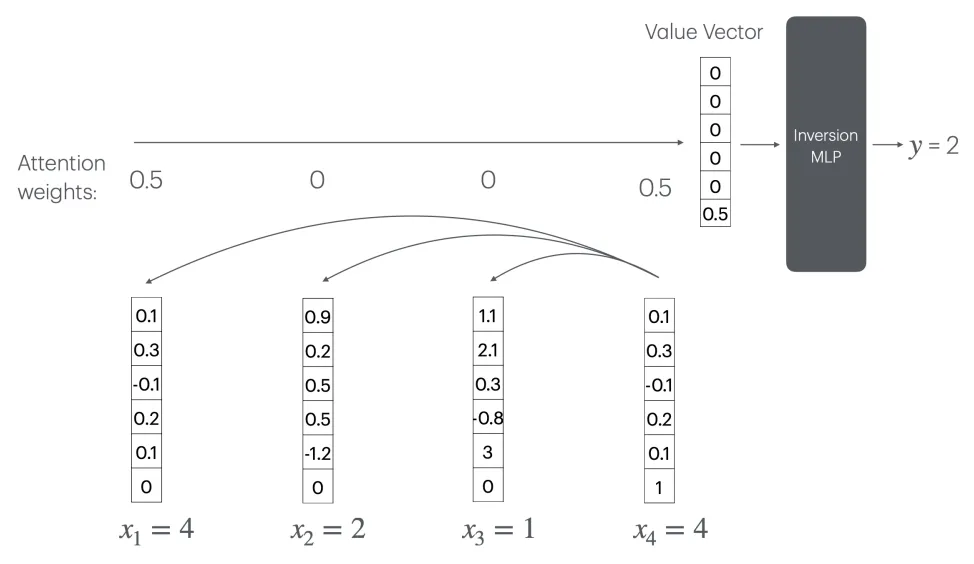
当嵌入维度不足时,词向量无法保持正交性,从而无法实现词频的线性叠加。此时,Transformer 可以通过注意力机制(CountAttend)来实现计数功能,但这需要一个随着序列长度 n 线性增长的大型“逆转MLP”层。
具体来说,模型首先通过注意力机制为查询词分配较大权重,并利用位置编码将注意力权重提取到值向量的最后一个元素中。该元素实际上记录了查询词出现频率的倒数。这要求模型具有一个大小为 O(n) 的 MLP 层来计算 1/x 函数(其中 x 是某个词的出现次数)。
然而,进一步分析表明,在神经元数量为 o(n) 的情况下,任何常数层 ReLU 网络都无法逼近 1/x 函数。因此,对于固定规模的 Transformer 模型,这种方法无法推广到任意长度的序列。当序列长度超过训练集中的长度时,模型的计数能力会急剧恶化。
为了验证这一结论,研究者进行了两个实验。首先,在一个从头开始训练的 Transformer 模型上进行了实验,具体参数如下:
- 训练和评估数据通过随机采样生成。
- 首先从大小为 m 的词汇表中均匀采样 n 个词,组成一个长度为 n 的序列。
- 序列长度 n 设置为 n = 10m,每个词平均出现 10 次。
- 共使用了 1600 个样本进行测试。
研究发现,随着词汇量的增加,模型的计数准确率呈阶梯状下降,临界点恰好出现在词汇量超过嵌入维度的时候。
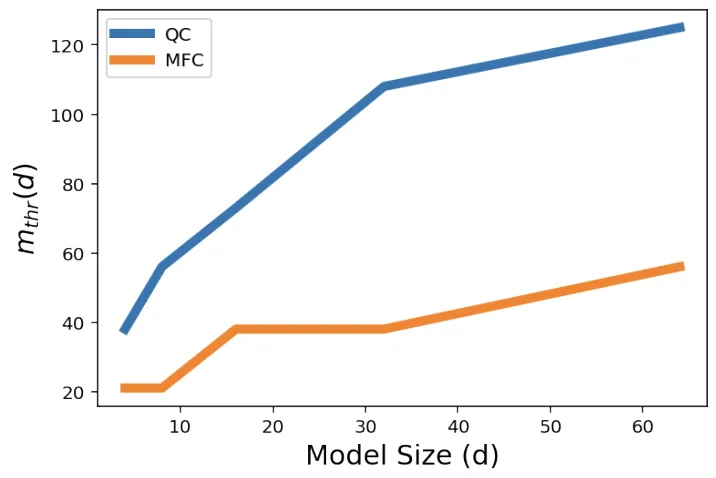
为了进一步量化模型的计数能力,研究者定义了一个指标 m_thr,即模型的计数准确率下降到 80% 时的临界词汇量。直观地讲,m_thr 反映了在给定嵌入维度下,模型可以“承受”的最大词汇量;m_thr 越大,说明模型的计数能力越强。
研究结果表明,在计数(QC)和识别最高频词(MFC)的任务中,m_thr 随着嵌入维度 d 的增加而近似线性增长。
在第二个实验中,研究人员使用了预训练的 Gemini 1.5 模型,重点关注词汇量对计数能力的影响。为此,他们设计了一系列计数任务,每个任务使用不同大小的词汇表,并且将每个词在序列中的平均出现次数保持恒定。这意味着,随着词汇量的增加,序列的长度也会相应变长。
为了进行对照,研究人员还设置了“二元基线”(Binary Baseline),即词汇表中只有两个固定词汇,但序列长度与主要实验组相同。这样可以区分导致模型计数误差的因素是词汇量还是序列长度。
实验结果显示,随着词汇量的增加,Gemini 1.5 在计数任务中的平均绝对误差显著上升,而“二元基线”的误差相对较低。
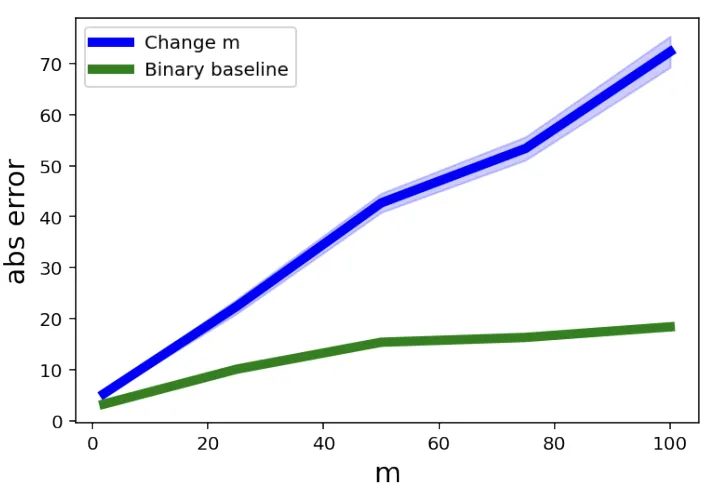
这表明,词汇量的增加,而不是序列长度的增长,是导致大模型计数能力下降的主要原因。尽管如此,研究人员指出,虽然这项研究在一定程度上划定了大模型计数能力的上下限,但这些界限还不够精确,离理想结果仍有差距。此外,他们尚未探讨增加 Transformer 层数是否会影响这一结论,需要未来开发新的技术工具来进一步验证。
论文地址:https://arxiv.org/abs/2407.15160

该研究将进一步增强大模型对小度产品的支持。
以下是重写的文本:
 还是中科大少年班校友
还是中科大少年班校友

已成功完成百亿参数规模模型的内部测试

大模型与软件测试综述发布
满足LLM在更多应用场景中的需求

大模型在“指令冲突”检测方面的新基准